写在前面：本章主要讲了现实中总是充满许多约束条件以及在这些条件下求解最优化策略的方法，并且着重讲了Slover工具，这里我也主要讲一下这个Slover求解器的运用。

第三章 最优化-寻找最大值

一、约束条件与最优化

你能控制的事物往往受到约束条件的限制，约束条件不会告诉你在解决问题过程中如何找到最佳策略，但是会告诉你在此过程中无法做到的事。

一般有约束条件时，会出现最优化问题，即在约束条件下该问题有最优解。如一根固定长的绳子，其围出的最大面积是多少。

二、借助目标函数发现问题

一般目标函数形式为：

P=C1X1+C2X2+……

其中： P为所求目标；C1、C2为约束条件；X1、X2为约束条件下的控制参数。

事实上，只需要这个函数帮助我们找出所求的问题及相关的一些参数即可，不是非得用这个函数计算。如：总利润=产品1利润+产品2利润-总成本，此时要找出产品1、产品2最大利润与最小总成本，这在现实中总会存在一些约束条件，如销量、原料等的限制，此函数就能使我们更快发现问题与求解方法。

三、图像法与Slover

这里我用书中的例子来举例。某玩具工厂在一个月的时间里最多能生产出400只橡皮鸭和300只橡皮鱼，每只橡皮鸭和橡皮鱼所需橡皮分别为100克和125克，每只橡皮鸭利润5元，每只橡皮鱼利润4元。现在该工厂有橡皮50000克，该工厂在一个月内分别生产多少橡皮鸭和橡皮鱼能有最大利润，其最大的利润为多少？

1.采用图像法计算

①最多能生产400只橡皮鸭和300只橡皮鱼，如图，即产品组合在黑色虚线范围内。

②有50000克橡皮，每只橡皮鸭和橡皮鱼分别消耗100克和125克，即最多能生产500只橡皮鸭或400只橡皮鱼。如图，即原料足够支撑的范围在蓝色实线范围内。

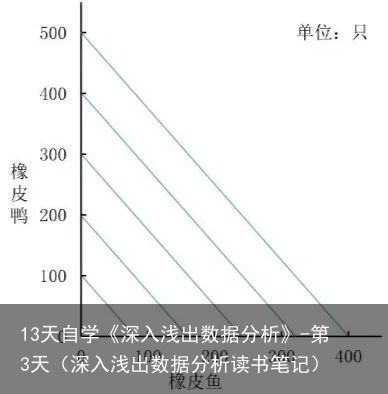
③将两个条件组合在一起，如图，即阴影部分为所有的产品组合方式。

④每个橡皮鸭利润5元，每个橡皮鱼利润4元，总利润=橡皮鸭数量x每个橡皮鸭利润+橡皮鱼数量x每个橡皮鱼利润。

观察公式可知，要使得利润最大，应该使达C1到最大，同时在C1最大的基础上尽可能的让C2也更大，最终获取最大利润。观察图像可得，橡皮鸭数量C1的最大为400只；当橡皮鸭数量为400只时，通过计算可得橡皮鱼数量C2为80只。

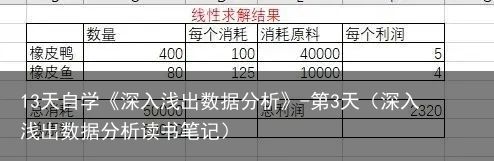
⑤当生产400只橡皮鸭，80只橡皮鱼时利润最大，最大利润2320元

2.借助Slover工具

我以excel2019为例，计算上面所说的例子。

①启用Slover工具（某度可查）

打开excel→左上角“文件”→“选项”→“加载项”→管理：excel加载项“转到”→勾“选规划求解加载项”→点击“确定”→回到excel界面点击菜单栏“数据”→右上角有一个“分析：规划求解”标签，表示已启用Slover。

②输入数据

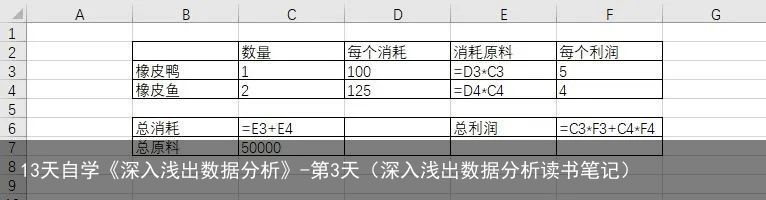
将所有数据输入excel中，注意由于规划求解器中无法进行运算，所以要把所有运算过程的写进单元格内才行。如：

实际上橡皮鸭和橡皮鱼的数量是我们要计算的变量，可以不用写，我这里写是为了方便大家能看清公式。另外再贴一张公式图。

③打开规划求解器输入数据

在选项卡数据栏右侧点击“规划求解”打开，弹出以下对话框。

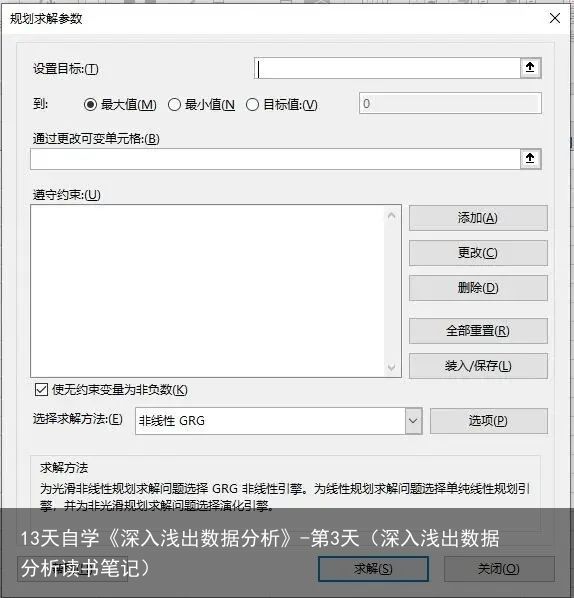
1.设置目标，即所求解的单元格，我这里是F6，点击F6单元格；

2.最大值/最小值/目标值，这次所求为最大值；

3.通过可改变单元格，即变量所在单元格，本次变量为两种产品数量，直接框选数量所在单元格C3和C4（这里鼠标左键同时框选与按住shift或ctrl分别点击C3、C4效果相同）。

4.添加约束，这次的约束条件有3个：橡皮鸭数量小于等于400、橡皮鱼数量小于等于300、总消耗不超过总原料量。这里以总消耗不超过总原料为例：点击“添加”，弹出对话框。

单元格引用即被约束的单元格，这里是总消耗单元格C6，点击C6；中间有多种约束可以选择，本次约束条件是小于等于总原料的数量50000，这里可以直接输入50000或者点击总原料量的单元格C7，我选择点击C7；接下来点击“确定”或者“添加”即添加完成（点击“确定”即返回并将该约束条件添加至规划求解对话框，点击“添加”将该约束条件添加至规划求解对话框但不返回，仍然留在添加约束对话框）。

约束添加完毕，如下图。

接下来点击“求解”，然后弹出对话框直接点确定就行了。

选择非线性GRG求解方法与选择单纯线性求解方法在这次计算中结果都差不多，但是选择非线性的话会有一点小偏差，具体原理是什么我还没弄明白，给大家看看两种结果。

这个工具还有很多种用法，大家慢慢的发掘吧。

四、负相关

即一个变量增多导致另一个变量减少，生活中大多数情况是如此。在进行分析计算的过程中，要多假设两个变量的相关性，并且全面的考虑到约束条件。

例如在前面例子中，分析过后调整橡皮鸭和橡皮鱼的产量能使利润最大化，仅仅是从生产端进行考虑，即生产多少就能出售多少。实际上情况并非如此，橡皮鱼和橡皮鸭的销售数量都受到约束，我们需要把新的约束条件考虑进去，再重新进行一次分析计算，以得到最优化的方案。

写在最后：由于个人原因，本系列将会停更几天，恢复时间待定，本人承诺尽快续写，感谢关注。另外知乎上面公式我无法打出来（虽然很简单），可去公众号查看。