NBA的比赛数据真的很适合做数据分析、数据可视化方面的练习，建议大家在kaggle上下载原数据自己试一试

NBA shot logs | Kaggle

。

一个月前写了一篇“用R语言进行NBA赛况分析”用R语言进行NBA赛况分析 - 专栏，这篇算是续篇，进一步发掘一些更有价值的数据，没看过上一篇的朋友建议先看一下上一篇文章，了解数据原的大概内容。

设立目标：

数据预处理：

本次分析还要用到我们上一篇中用过的几个工具包，和自定义的两个函数，所以先加载相应代码（具体参见用R语言进行NBA赛况分析 - 专栏)：

#加载包 library(dplyr) library(magrittr) library(ggplot2) library(ggthemes) library(reshape2) #定义函数，用于计算后面每位球员的2分球命中次数 two_get<-function(x){ count<-length(x) n<-0 for(i in 1:count){ if(x[i]==2) n<-n+1 } return(n) } #定义函数，用于计算后面每位球员的3分球命中次数 three_get<-function(x){ count<-length(x) n<-0 for(i in 1:count){ if(x[i]==3) n<-n+1 } return(n) }

本次分析要针对128069条的所有观测，分析的对象是所有球员，所以首先将12万条数据根据不同球员进行分组统计，得到我们想要的变量：

#统计每位球员的投篮次数、命中次数、总得分、1分2分3分命中次数 by_name<-group_by(shot_logs,player_name)%>% summarise(count=n(), made_num=sum(FGM), points=sum(FGM*PTS_TYPE), three_pts_num=three_get(as.numeric(PTS)), two_pts_num=two_get(as.numeric(PTS)), one_pts_num=made_num-two_pts_num-three_pts_num)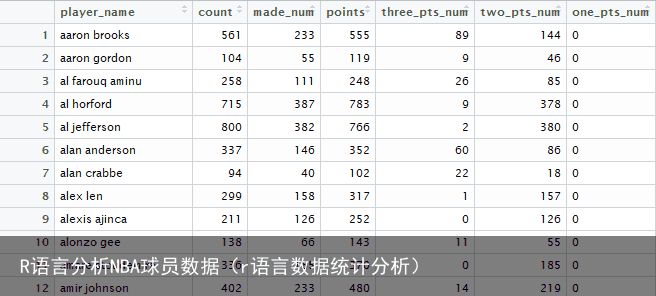看来数据里不包括罚篮（1分球）......

目标1：线性分析

我们想知道球员的出手次数和得分是否线性相关、相关的强弱程度，可以把count变量作为自变量，points变量作为因变量，用lm()函数做一个简单的一元线性回归：

> revelant<-lm(by_name$points~by_name$count,data = by_name) #用summary()函数得到相关参数 > summary(revelant) Call: lm(formula = by_name$points ~ by_name$count, data = by_name) Residuals: Min 1Q Median 3Q Max -125.019 -22.961 -3.369 17.396 169.290 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 0.11594 5.41983 0.021 0.983 by_name$count 0.99706 0.01062 93.876 <2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 40.86 on 279 degrees of freedom Multiple R-squared: 0.9693, Adjusted R-squared: 0.9692 F-statistic: 8813 on 1 and 279 DF, p-value: < 2.2e-16 #用plot()函数绘制图形 > plot(by_name$count,by_name$points, + xlab = count,ylab = points) > abline(revelant)根据summary()函数得到的参数我们可以看到，两个变量之间的相关系数是0.997，P值为2e-16远远小于0.05，而R-squared判定系数为0.969（表示回归直线可解释96.9%的总变差），说明两者显著相关，从图上也可以看出其相关性非常好，散点基本落在直线两侧，这也说明教练对于球员上场的安排情况十分合理，不存在投篮次数过多而得分较少或者得分很高但是投篮机会却很少的情况。

目标2：

查看总得分前五名的球员和出手次数前五名的球员：

#得分前五 by_name.1<-by_name[order(-by_name$points),] by_name.1<-by_name.1[1:5,]#出手次数前五 by_name.2<-by_name[order(-by_name$count),] by_name.2<-by_name.2[1:5,]

目标3：

得分前五名的球员在不同距离的投篮和命中情况：

#从数据原中挑出前五名球员的完整数据 data.1<-filter(shot_logs, player_name==mnta ellis| player_name==lebron james| player_name==klay thompson| player_name==james harden| player_name==stephen curry) #根据不同球员的投篮次数和命中次数绘制分面直方图 ggplot(data=data.1,aes(SHOT_DIST,fill=factor(FGM)))+ geom_histogram()+ facet_grid(.~player_name)+ theme_few()可以根据图形猜测一下，stephen curry（库里）的表现相对来说是比较稳定的，而lebron james（詹姆斯）则在三分线内表现较好，下面我们用更直观的方式来检验我们的猜测。

目标4：

得分前五名的球员命中的2分球和3分球所占比例：

#只留下命中的数据 data.2<-filter(data.1,data.1$FGM==1) #根据得分情况绘制堆叠图 ggplot(data = data.2,aes(x=player_name,fill=factor(PTS)))+ geom_bar()+ theme_few()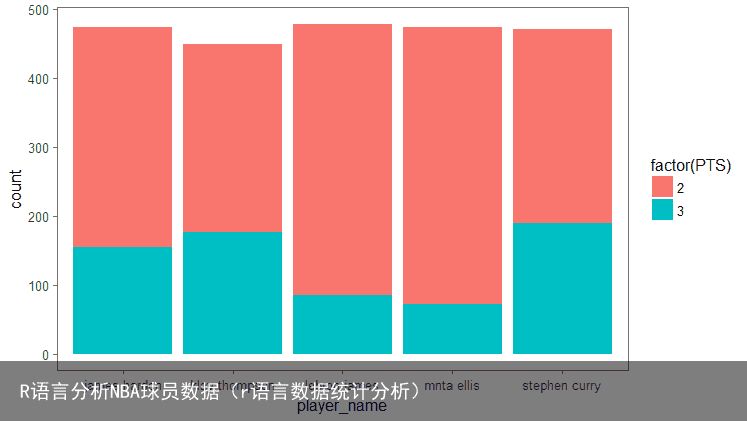看以看到的确是stephen curry（库里）的三分和二分比例最协调，而lebron james（詹姆斯）二分命中次数更多一些。

这里画图的时候遇到了一个BUG......本来的想法是直接统计出五个球员三分的命中次数添加到五条观测里，再进行绘图，但是尝试了半天好像画图时没办法实现，最后只能根据名字筛出全部数据，然后利用ggplot绘图时自带的count功能进行绘制。

目标5：

密度图表示得分前五名的球员命中次数随距离变化情况，实际上就是把目标3里直方图的蓝色部分画的平滑一些，这样更便于观察，但是没有添加颜色，所以美观度看起来就差了一些：

ggplot(data=data.2,aes(x=SHOT_DIST))+ geom_density()+ facet_grid(player_name~.)+ theme_few()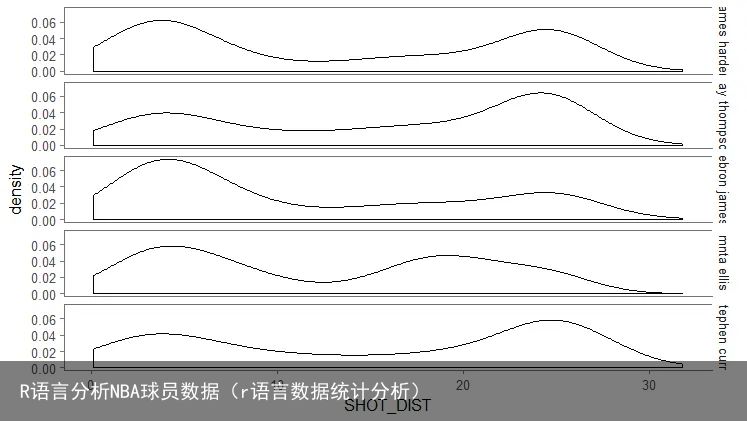比赛数据还有很多值得分析的地方，强烈建议大家自己动手试一试，同时还可以锻炼数据思维。