看过深入浅出系列的人，应该知道这一系列的书通常趣味性挺强的，但干货不多。不过《深入浅出数据分析》还是可以读一读的，因为这是一本偏商业分析的书籍，每个章节都是一个商业分析案例，从拿到问题开始，一步步展示数据分析师是如何思考问题的，这是本书一大亮点，很值得学习。另外书中会零零散散的介绍一些excel函数和R语言的语法，我觉得这部分还是看专业书籍比较好，就不做详述了。

第一章 分解数据

知识点：

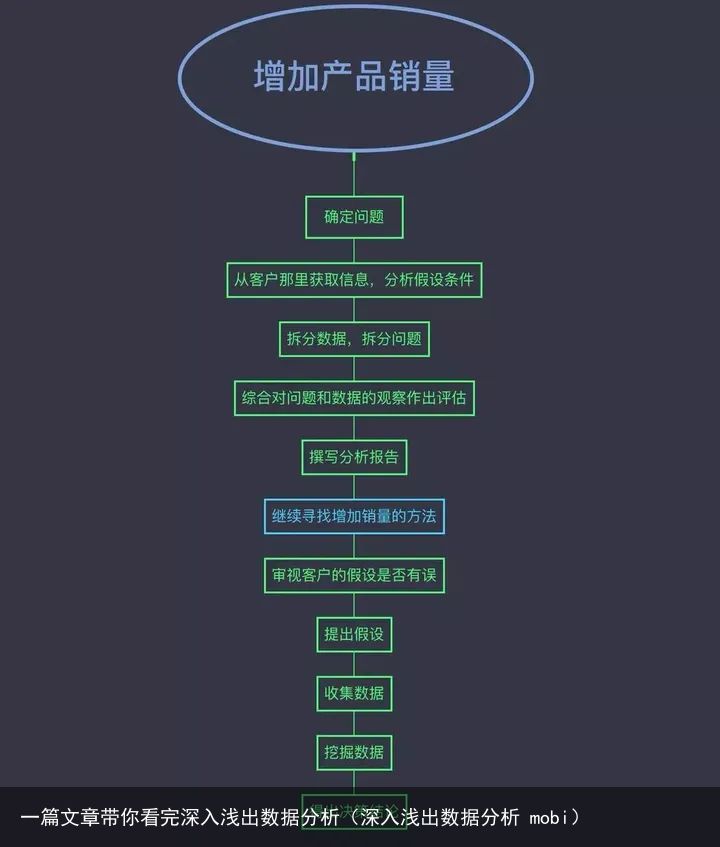
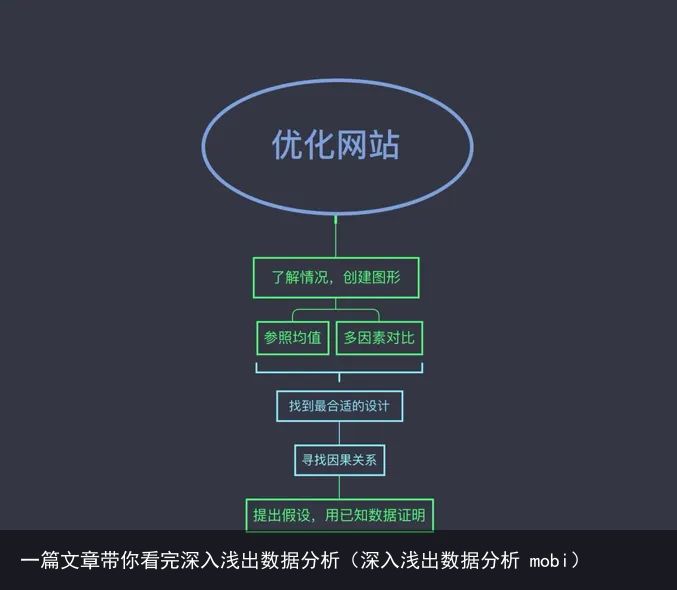
几乎所有的分析思路就是这个样子，在实际操作过，可能会一遍一遍循环上述过程，直到达到目标。

确定问题：通常需要从客户那里多了解一些信息，以便我们确定问题。但是有时候客户也是不了解问题或者目标的，因此需要分析师甄别客户提供的与实际情况不符的信息。也就是不能全听客户一面之词，要靠数据说话。

如何提问：

问目标：销量提高多少问是多少：这样就可以得到一些可以量化的数据问竞争对手的情况问预算

从客户的回答里面可以找到很多基础假设，这些都是分析的基础。

分解：就是将大问题分解到小问题，大块数据分解到更小的组块。尝试分解的重要因子是找到比较对象。然后分解汇总数据。

评估组块：总结客户的假设观点和对数据观察结果，两者进行比较，作出合理的推测。

决策报告：将设想和判断结合起来作出一份报告。

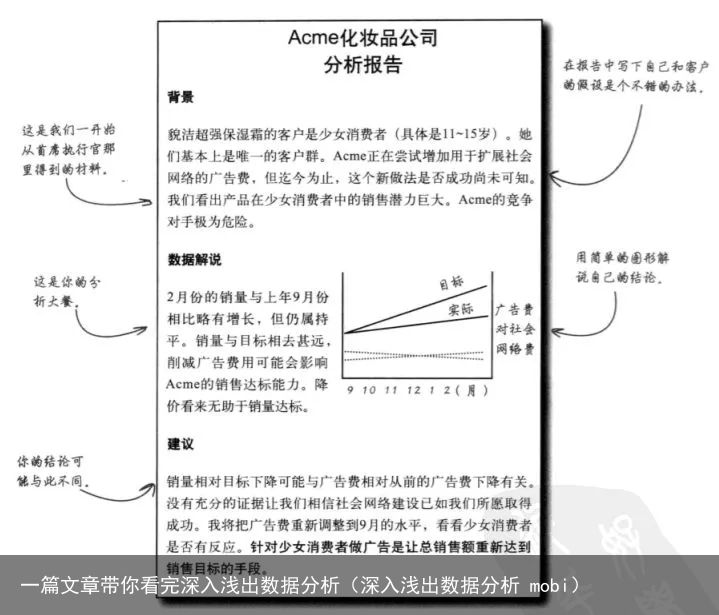
有时候客户的假设不一定正确，要根据数据进行修正。重点是要找到不确定的因素进行再次分析和挖掘。

案例分析：

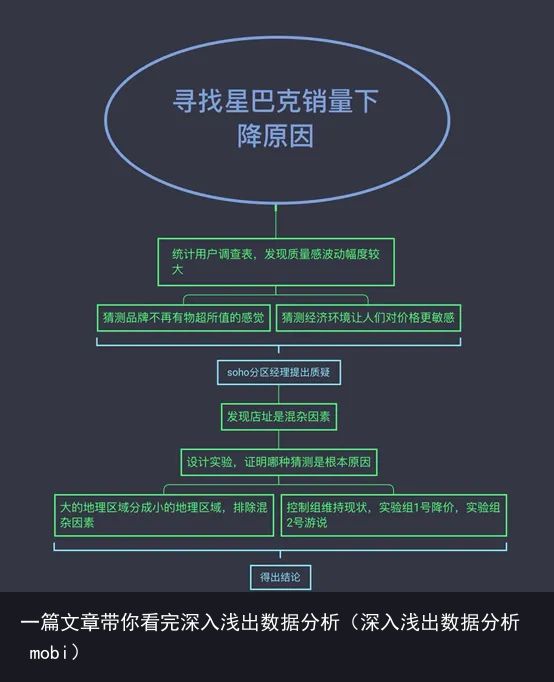
第二章 实验

知识点：

比较法：比较是破解观察数据的法宝。

混杂因素：研究对象的个人差异，它不是试图进行比较的因素，最终会导致分析结果的敏感度变差。要分析并校正混则因素。

控制组：实验需要控制组和对照组，没有控制组就意味着没有比较。确保两个组仅有一点不同，其他因素要一致。

选择相似性：在同一类大的数据集里，随机挑选小数据集，并分配实验组和控制组，将保证除了研究变量不同外，其余变量基本一致。

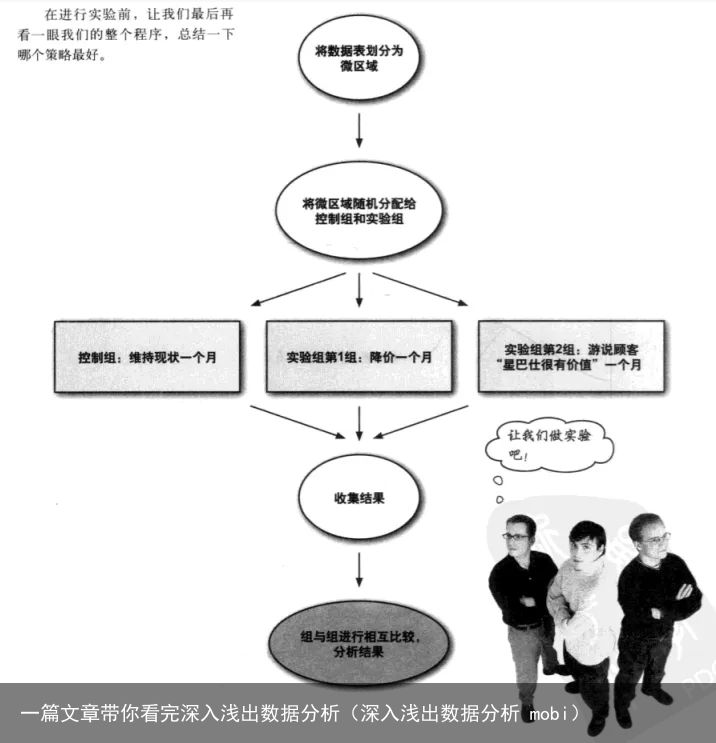
案例分析：

第三章 最优化

知识点：

约束条件和决策变量：约束条件就是无法控制的因素，如单位时间生产量。决策变量是可控因素，目标就是在不超出约束条件的情况下，对决策因素做一个组合，实现最大利润。

最大化问题：将决策变量，约束条件和希望最大化的目标合并成一个目标函数。任何最优化问题都有一些约束条件和目标函数。

可行区域：产品组合所在由约束线围城的空间。如约束条件：橡胶供应量能产生500只橡皮鸭和400条橡皮鱼。时间够用来生产400只橡皮鸭或300条橡皮鱼。

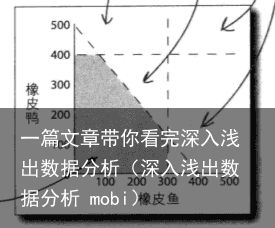
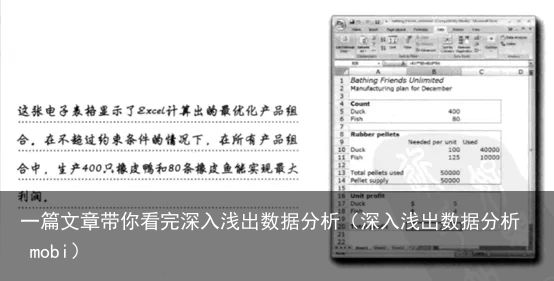
负相关性：一种产品越多就意味着另一种产品减少。不要假定两种变量是不相关的，创建模型时，要规定假设中的各种变量的相互关系。

时效性：情况总是变化，因此模型也不是一尘不变的，需要经常根据实际情况进行修正。

案例分析：

第四章 数据图形化

知识点：

数据图形的原则：

展示了数据作了高明的比较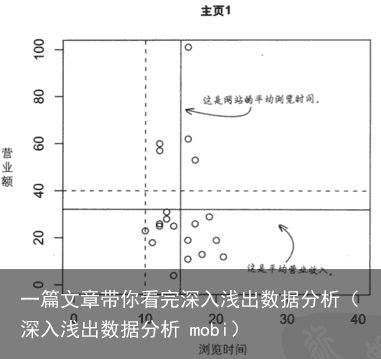展示了多个变量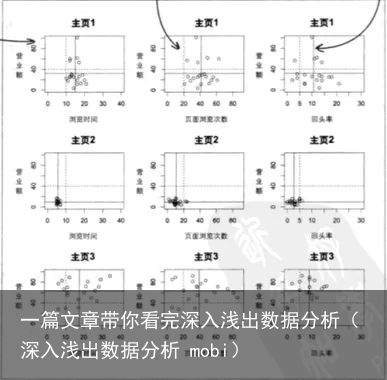

从图形上可以直观的看出假设与数据是否相符。

案例分析：

第五章 假设检验

知识点：

变量相关性：若一种变量增大另一种变量也增大，则是正相关，一种增大一种减小则是负相关。

证伪法：剔除无法证实的假设。

满意法：选出看上去最可信的第一个假设的做法。

进行假设检验要使用证伪法，回避满意法。

当证据不充分时，无法进行排除时，应该对假设进行评级，将不利证据越少的排在前面。

案例分析：

第六章 贝叶斯检验

知识点：

假阳性，真阳性:

条件概率：以一件事的发生为前提的另一件事的发生概率。

贝叶斯规律：

贝叶斯规律可以反复使用，每当产生了一个新的概率，就可以把新的概率当成基础概率，不停的迭代验算。

第七章 主观概率

知识点：

主观概率：用数字形式的概率表示自己对某事的确认程度。举例：我相信俄罗斯支持石油业的概率是60%。主观概率是根据规律进行分析的巧妙方法，尤其在预测孤立事件却缺乏从前在相同条件下发生过的事件的可靠数据的情况下。

标准偏差：分析点和数据集平均值的差距。任何一个数据集的大部分观察数据都会落在平均值的一个标准偏差范围内。可以用标准偏差度量分析，标准偏差越大，分析就越大。

贝叶斯规则：贝叶斯规则也可以用来修正主观概率，找出假设成立的条件下，证据出现的概率。

案例分析：

第八章 启发法

知识点：

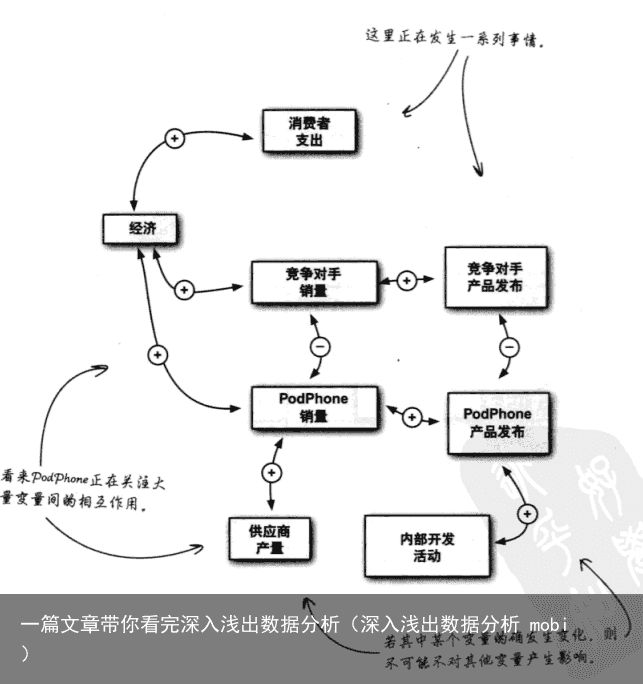
用量化理论了解变量之间的作用：

启发法：上面的问题，一开始没有思路解决，可以从增加几个变量开始。根据这些变量对整个系统作出结论，据此做出评价。启发法是从直觉走上最优化的桥梁。

快省树：

案例分析：

第九章 直方图

知识点：

直方图可以展示数据频数分布情况

利用数据子集进行比较，往往能有所发现。

第十章 回归

知识点：

预测是数据分析的重头戏。把假设检验和预测加起来就等于数据分析。s

散点图：显示两种变量的关系。

回归线：将所有数据画在散点图上以后，最准确贯穿平均值图中各个点。回归线可以用线性方程y=a+bx表示。

相关性：两种变量之间的线性关系。相关性可强可弱，用相关性系数r表示。R的范围为-1至1，0表示无相关性，1和-1表示两个变量完全相关。

第十一章 合理误差

知识点：

外插法：用回归方程预测数据范围以外的数值。因为缺乏相应的数据无法准确判断，应该指定附加假设条件，明确表示不考虑数据集发生的情况。

残差：实际结果与预测结果之间的偏差。定量的指定误差反而能让你的预测结果更精准。

回归线的均方根误差：实际结果与典型预测结果之间的差距。

均方根误差与标准差的区别。标准差度量的是某一个变量，通常描述平均值周围的分布情况。

而均方根误差指出的是两个变量之间的关系，描述的是回归线周围的分布情况。

当发现单独使用一个模型时，某一个数据段估计误差太高，而另一段又太低时，可以将数据分段。优秀的回归分析应该兼具解释功能和预测功能，这有点像统计学里的，不能过拟合也不能欠拟合。

调整为两段后

案例分析：

第十二章和第十三章讲的是数据库和数据整理（Excel），需要学习的可以参考更加专业的书籍。

关注个人公众号：与YY共勉