《数值分析》这门课从某种程度上可以说决定了我以后的学习，对她有很深的感情，所以我想谈谈自己的拙见~~

====================

去年这会儿我们也上数值分析，刚好也有大作业要做。和题主不一样的是，第一节课我就喜欢这门课了。还记得老师举了一些计算思维的例子，印象最深的就是迭代（iteration）了，一个方程可以通过x=f(x)这种方式进行迭代求解不是很巧妙吗？再比如局部近似里的以直代曲其实就是数值积分的思想，而不断的局部以直代曲，就是非线性方程牛顿法的思想。还有其他一些思想，比如外推法等等...那次课让我觉得计算数学也很神奇~~

科学研究方法可以分为理论分析、科学实验、科学计算。理论分析和科学实验大家比较熟知，那什么是科学计算呢？许多复杂的问题需要借助计算机快速准确的数据处理能力，用计算机处理数值问题的方法就是所谓的科学计算。数值分析这门课的主旨就是将分析问题代数化，培养计算思维，研究如何借助计算工具求得数值问题(问题本身反映了初始数据和要求的数值型数据之间的某种确定性关系）的数值解。其实有数学以来就有数值计算，只是在计算机出现前它的理论和发展很缓慢而已。

题主问到数值分析在现实中有哪些应用？那我们先整理下用数学解决实际问题的步骤，一般有以下几步：

1.根据实际问题建立数学模型——应用数学

2.数学模型分析(比如模型解的存在、唯一、适定性）——基础数学

3.针对相应的数值问题设计可靠高效的算法

4.计算结果可视化

5.计算结果分析

我觉得后面三步其实都可以划分到数值分析里，而这门课的核心即是设计高效可靠的算法。

下面说些题主想知道的实际应用吧~

凡是涉及到计算的地方几乎都需要数值分析，比如天气预报，比如工程设计，比如楼上很多人说的流体固体计算，比如核武器的研制，比如导弹和火箭的发射等等。（有没有觉得很有用呢^o^）真的没有夸大其词，因为这些问题大都会涉及方程组(线性，非线性，微分)的求解，而多数情况下是无法给出解析解的。所以需要考虑

（级数解法，逐次逼近法）和

（给出一些离散点处解的近似值），而这不正是数值分析研究的内容么？

具体说下我比较感兴趣的两个应用~

1）天气预报：天气会受各种因素的影响，稍微一些因素发生改变就会产生很大的变化，所以天气预报其实是一件比较困难的工作（我们就不要太抱怨天气预报不准了哦O(∩_∩)O）古代人们用占卜或者经验总结等方式来预计天气状况，这倒更像是统计学。而有了计算机，我们就可以通过数值模拟来预报天气。具体过程就是：首先根据大气运动列出数学物理方程（偏微分），其次对空间进行网格划分，然后通过观测数据给出初值条件，最后通过数值方法求解这些偏微分方程得到网格点处的数值解。这也是为什么主持人总是说大概在...地区，大致在...时段，可能有...量级的降水...因为时空是连续的，而网格划分不可能无限密，所得的数值解也存在误差~

2）等离子体：对等离子体现有的理论描述中，磁流体力学、符拉索夫方程、福克-普朗克方程等都是微分方程，包含很多参量，如果要求出解析解，物理模型往往需要过分简化以至于无法精确和全面的包罗各种效应，所以需要数值计算，这也是等离子体物理学研究中很重要的一个方面。比如最简单的单粒子模型，它的牛顿洛伦兹方程是这样：

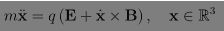
你看，这不就是一个二阶微分方程么？所以你可以用数值分析里的隐式欧拉，显式欧拉，中点格式，龙格库塔等方法来求解。当然你也可以设计自己的算法~~

我一直认为，每门数学课都像是一个个栩栩如生的人物，都有自己鲜明的个性，他们之间也有着很多联系。要想学好一门课，首先要了解他的特点。整本数值分析书看上去充斥着一个个数值算例，活生生的一本应用数学教材，可其中也有很多有价值的思想。说几个我感悟到的吧(*^__^*) ……

1>主要矛盾和次要矛盾之间的关系；现实问题中有很多约束条件，需要我们有侧重的保留摒弃，辨析主要矛盾和次要矛盾，从而提出合理假设~

2>尺有所短寸有所长；没有完美无缺的算法，虽然我们看到有不断地改进优化算法，但这些往往都是以牺牲某些优点为代价的。比如提高精度，往往会导致格式复杂，产生较大运算量~

3>原则不能变；算法也是要讲原则的，比如要谈算法的优劣性前提是要保证算法的可靠性（相容、收敛、稳定等）~

其实，只要用心体会，会有很多收获，不仅仅是数学上的，有时何尝不是一种人生感悟呢~~

====================

不积跬步，无以至千里；不积小流，无以成江海。厚积方能薄发，再高深的应用都源自于一道道不起眼的练习题。感觉枯燥并不可怕，可怕的是耐不住这份枯燥，所以认真推导每一个格式，认真思考每一个算法，认真编写每一段代码，会发现不仅仅是数值分析，所有数学课都有他的用武之地。与题主共勉~~