探索性数据分析（EDA）是任何数据分析或数据科学项目中的重要一步。EDA 是调查数据集以发现模式和异常（异常值）并根据我们对数据集的理解形成假设的过程。

EDA 涉及为数据集中的数值数据生成汇总统计数据，并创建各种图形表示以更好地理解数据。在本文中，我们将借助示例数据集了解 EDA。为此，我们将使用Python语言（Pandas库）。

导入库

我们将从导入执行 EDA 所需的库开始。其中包括 NumPy、Pandas、Matplotlib 和 Seaborn。

import numpy as np import pandas as pd import matplotlib.pyplot as plt %matplotlib inline import seaborn as sns

读取数据

我们现在将 CSV 文件中的数据读入 Pandas DataFrame。

让我们看看我们的数据集如何使用 df.head()。输出应如下所示：

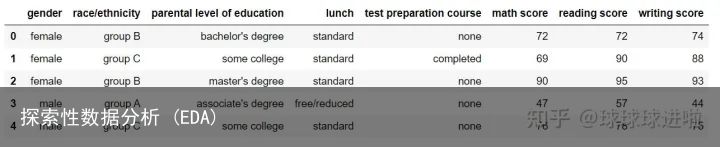
描述性统计

完美的！数据看起来就像我们想要的那样。您可以通过查看数据集轻松判断它包含有关学校/学院不同学生的数据，以及他们在 3 个科目中的分数。让我们从查看数据集的描述性统计参数开始。我们将为此使用 describe()。

df.describe(include=all)

通过为包含属性分配“全部”值，我们确保分类特征也包含在结果中。输出 DataFrame 应如下所示：

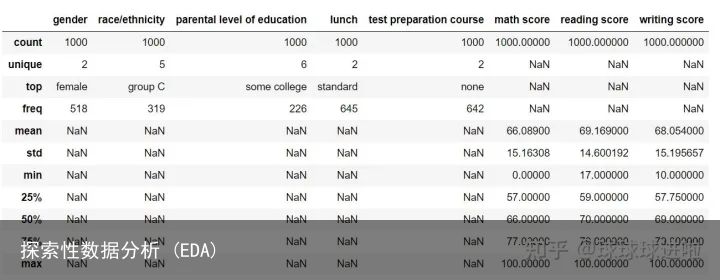
对于数值参数，已填充平均值、标准差、百分位数和最大值等字段。对于分类特征，已填充计数、唯一性、顶部（最常见的值）和相应的频率。这让我们对我们的数据集有了一个广泛的了解。

缺失值插补

我们现在将检查 数据集中的缺失值。如果有任何缺失的条目，我们将用适当的值（分类特征的模式，以及数字特征的中位数或平均值）来估算它们。为此，我们将使用 isnull() 函数。

df.isnull().sum()

这将告诉我们数据集中每列中有多少缺失值。输出（Pandas 系列）应如下所示：

对我们来说幸运的是，这个数据集中没有缺失值。我们现在将继续分析这个数据集，观察模式，并在图形的帮助下识别异常值。

图示

我们将从单变量分析开始。为此，我们将使用条形图。我们将研究学生在性别、种族/民族、午餐状况以及是否有备考课程方面的分布。

plt.subplot(221) df[gender].value_counts().plot(kind=bar, title=学生性别, figsize=(16,9)) plt.xticks(旋转=0) plt.subplot(222) df[race/ethnicity].value_counts().plot(kind=bar, title=学生的种族/民族) plt.xticks(旋转=0) plt.subplot(223) df[lunch].value_counts().plot(kind=bar, title=学生午餐情况) plt.xticks(旋转=0) plt.subplot(224) df[备考课程].value_counts().plot(kind=bar, title=备考课程) plt.xticks(旋转=0) plt.show()

输出应如下所示：

我们可以从图中推断出很多东西。学校里的女生比男生多。大多数学生属于 C 组和 D 组。超过 60% 的学生在学校享用标准午餐。此外，超过 60% 的学生没有参加任何考试准备课程。

继续单变量分析，接下来，我们将对数据集中的数字列（数学分数、阅读分数和写作分数）制作一个箱线图。箱线图帮助我们根据四分位数可视化数据。它还识别数据集中的异常值（如果有）。我们将为此使用 boxplot() 函数。

df.boxplot()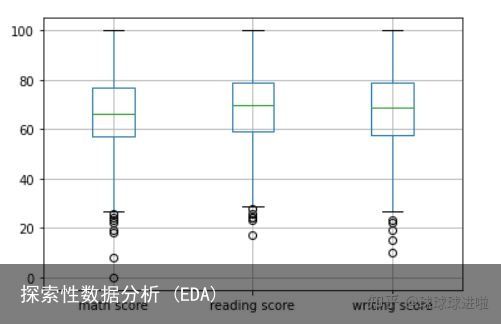

中间部分代表四分位间距（IQR）。中间的水平绿线代表数据的中位数。尾部附近的空心圆圈表示数据集中的异常值。但是，由于学生很有可能在考试中得分极低，因此我们不会删除这些异常值。

我们现在将绘制学生数学成绩的分布图。分布图告诉我们数据是如何分布的。我们将使用 distplot 函数。

sns.distplot(df[math score])

输出中的绘图应如下所示：

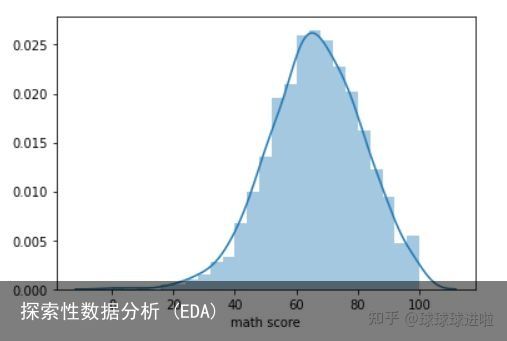
该图紧密地代表了完美的钟形曲线。峰值在 65 分左右，这是数据集中学生数学成绩的平均值。也可以为阅读分数和写作分数制作类似的分布图。

我们现在将借助热图查看 3 个分数之间的相关性。为此，我们将在本练习中使用 corr() 和 heatmap() 函数。

corr = df.corr() sns.heatmap(corr, annot=True, square=True) plt.yticks(rotation=0) plt.show()

输出中的绘图应如下所示：

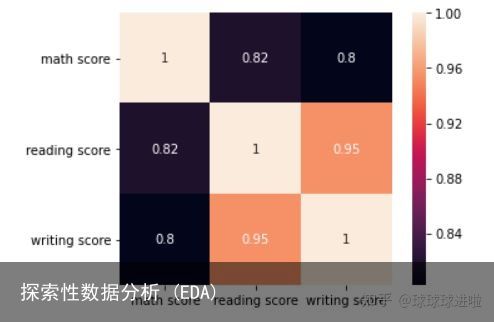
热图显示这 3 个分数高度相关。阅读分数与写作分数的相关系数为0.95。数学分数与阅读分数的相关系数为 0.82，与写作分数的相关系数为 0.80。

我们现在将继续进行双变量分析。我们将看一下 Seaborn 中的关系图。它有助于我们理解数据集不同子集上两个变量之间的关系。我们将尝试了解不同性别学生的数学成绩和写作成绩之间的关系

sns.relplot(x=math score, y=writing score, hue=gender, data=df)

关系图应如下所示：

该图显示了男女学生之间的分数明显差异。对于相同的数学分数，女学生比男学生更有可能获得更高的写作分数。但是，对于相同的写作分数，预计男生的数学分数要高于女生。

关系图帮助我们进行双变量分析。

最后，我们将根据父母的教育水平和备考课程来分析学生在数学、阅读和写作方面的表现。首先，让我们用线图来看看父母的教育水平对孩子在校表现的影响。

df.groupby(parental level of education)[[math score, reading score, writing score]].mean().T.plot(figsize=(12,8))

输出将如下所示：

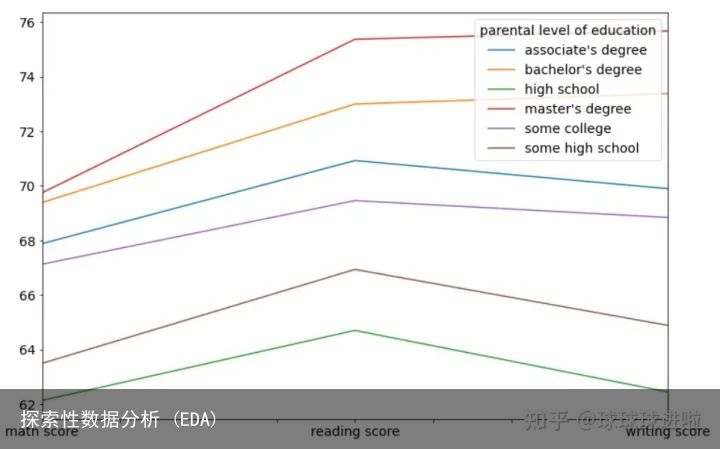
从这张图中可以非常清楚地看出，父母受教育程度高于其他人（硕士、学士学位和副学士学位）的学生的平均表现要好于父母受教育程度较低的学生（高中）。这可能是遗传差异，或者仅仅是学生在家环境的差异。受过良好教育的父母更有可能推动学生学习。

其次，我们用水平条形图来看看备考课程对学生成绩的影响。

df.groupby(test preparation course)[[math score, reading score, writing score]].mean().T.plot(kind=barh, figsize=(10,10))

输出应如下所示：

同样，很明显，与没有选择该课程的学生相比，完成考试准备课程的学生平均表现更好。

在本文中，我们借助示例数据集了解了探索性数据分析 (EDA) 的含义。我们研究了如何分析数据集，从中得出结论，并在此基础上形成假设。