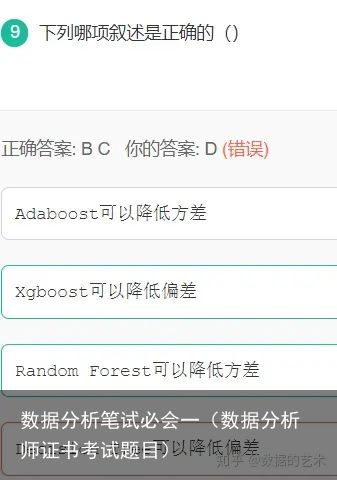
1.boosting算法

boosting算法是一种集成学习算法，由一些列基本分离器按照不同的权重组合为一个强分类器，这些基本分类器之间有依赖关系。包括adaboost算法，提升树，GBDT算法。

2.bagging算法：装袋算法（引导聚集算法）

作用:与其他分类回归，算法相结合，提高准确率，稳定性的同时，降低结果的方差，避免过拟合的发生。

思想：给定一个弱学习算法和一个训练集，单个弱学习算法准确率不高，将该弱学习算法试验多次，得出预测函数序列，进行投票。最后结果的准确率将的到提高。如：随机森林

3.判别式模型与生成式模型

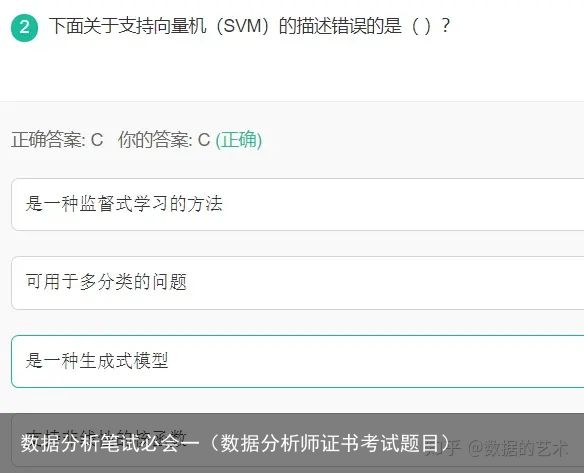
判别式模型（Discriminative Model）是直接对条件概率p(y|x;θ)建模。常见的判别式模型有 线性回归模型、线性判别分析、支持向量机SVM、神经网络等。（根据特征来判断类别）

生成式模型（Generative Model）则会对x和y的联合分布p(x,y)建模，然后通过贝叶斯公式来求得p(yi|x)，然后选取使得p(yi|x)最大的yi，即：（根据已经拥有的特征来建立模型，最后再使用模型来进行判断类别）

常见的生成式模型有 隐马尔可夫模型HMM、朴素贝叶斯模型、高斯混合模型GMM、LDA等。

4.EM算法：

EM 算法通过逐步提高极大似然的下限，以此求出极大似然函数对参数的估计，为无监督算法

EM（Expectation-Maximization）算法，称为期望最大值化算法，是无监督的算法。

EM算法解决这个的思路是使用启发式的迭代方法，既然我们无法直接求出模型分布参数，那么我们可以先猜想隐含数据（EM算法的E步），接着基于观察数据和猜测的隐含数据一起来极大化对数似然，求解我们的模型参数（EM算法的M步)。由于我们之前的隐藏数据是猜测的，所以此时得到的模型参数一般还不是我们想要的结果。不过没关系，我们基于当前得到的模型参数，继续猜测隐含数据（EM算法的E步），然后继续极大化对数似然，求解我们的模型参数（EM算法的M步)。以此类推，不断的迭代下去，直到模型分布参数基本无变化，算法收敛，找到合适的模型参数。

5.spass的交叉分析

spss中交叉分析主要用来检验两个变量之间是否存在关系，或者说是否独立，其零假设为两个变量之间没有关系。在实际工作中，经常用交叉表来分析比例是否相等。例如分析不同的性别对不同的报纸的选择有什么不同。

6.l1与L2正则化

L1和L2是正则化项，又叫做罚项，是为了限制模型的参数，防止模型过拟合而加在损失函数后面的一项。

区别：

　　L1是模型各个参数的绝对值之和。

　　　L2是模型各个参数的平方和的开方值。

L1会趋向于产生少量的特征，而其他的特征都是0. 因为最优的参数值很大概率出现在坐标轴上，这样就会导致某一维的权重为0 ，产生稀疏权重矩阵

L2会选择更多的特征，这些特征都会接近于0。最优的参数值很小概率出现在坐标轴上，因此每一维的参数都不会是0。当最小化||w||时，就会使每一项趋近于0

再讨论几个问题

为什么参数越小代表模型越简单？

越是复杂的模型，越是尝试对所有样本进行拟合，包括异常点。这就会造成在较小的区间中产生较大的波动，这个较大的波动也会反映在这个区间的导数比较大。

　　只有越大的参数才可能产生较大的导数。因此参数越小，模型就越简单。

实现参数的稀疏有什么好处？

因为参数的稀疏，在一定程度上实现了特征的选择。一般而言，大部分特征对模型是没有贡献的。这些没有用的特征虽然可以减少训练集上的误差，但是对测试集的样本，反而会产生干扰。稀疏参数的引入，可以将那些无用的特征的权重置为0.

L1范数和L2范数为什么可以避免过拟合？

加入正则化项就是在原来目标函数的基础上加入了约束。当目标函数的等高线和L1,L2范数函数第一次相交时，得到最优解。

　L1范数：

L1范数符合拉普拉斯分布，是不完全可微的。表现在图像上会有很多角出现。这些角和目标函数的接触机会远大于其他部分。就会造成最优值出现在坐标轴上，因此就会导致某一维的权重为0 ，产生稀疏权重矩阵，进而防止过拟合。

L2范数：

L2范数符合高斯分布，是完全可微的。和L1相比，图像上的棱角被圆滑了很多。一般最优值不会在坐标轴上出现。在最小化正则项时，可以是参数不断趋向于0.最后活的很小的参数。

　7.PCA的原理与易错点

主成分分析（Principal Component Analysis，PCA）， 是一种统计方法。通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量，转换后的这组变量叫主成分。在很多情形，变量之间是有一定的相关关系的，当两个变量之间有一定相关关系时，可以解释为这两个变量反映此课题的信息有一定的重叠。主成分分析是对于原先提出的所有变量，将重复的变量（关系紧密的变量）删去多余，建立尽可能少的新变量，使得这些新变量是两两不相关的，而且这些新变量在反映课题的信息方面尽可能保持原有的信息。依据方差最大的原则来构建主成分最经典的做法就是用F1（选取的第一个线性组合，即第一个综合指标）的方差来表达，即Var(F1)越大，表示F1包含的信息越多。因此在所有的线性组合中选取的F1应该是方差最大的，故称F1为第一主成分。如果第一主成分不足以代表原来P个指标的信息，再考虑选取F2即选第二个线性组合，为了有效地反映原来信息，F1已有的信息就不需要再出现在F2中，用数学语言表达就是要求Cov(F1, F2)=0，则称F2为第二主成分，依此类推可以构造出第三、第四，……，第P个主成分。PCA的应用

主成分分析能降低所研究的数据空间的维数

有时可通过因子负荷aij的结论，弄清X变量间的某些关系。

多维数据的一种图形表示方法。

由主成分分析法构造回归模型。即把各主成分作为新自变量代替原来自变量x做回归分析。

用主成分分析筛选回归变量。

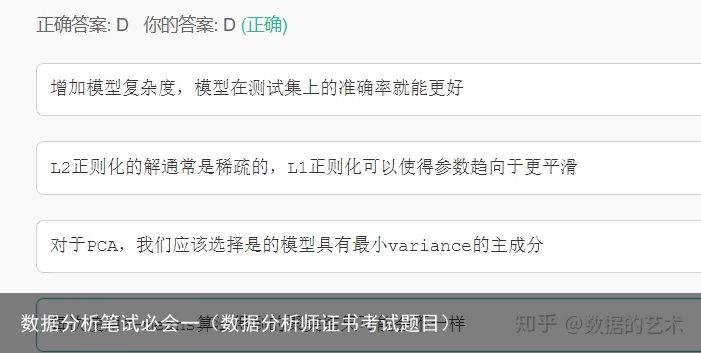
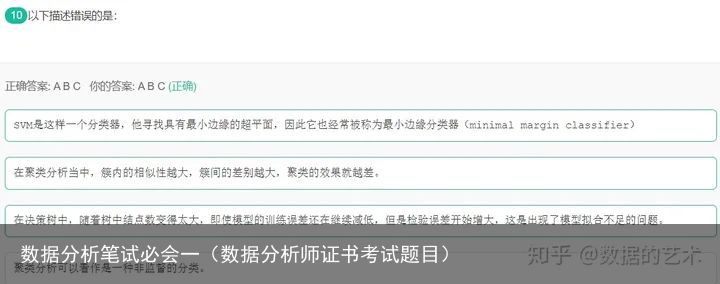
解析：SVM被称为最大间隔分类器

模型的训练误差降低，检验误差增大，这是出现了模型的过拟合现象

8.偏差与方差

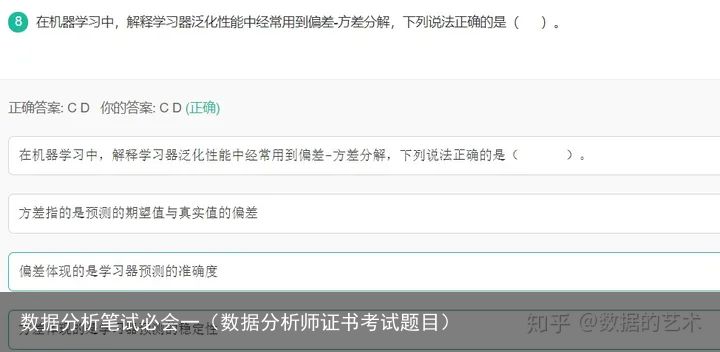
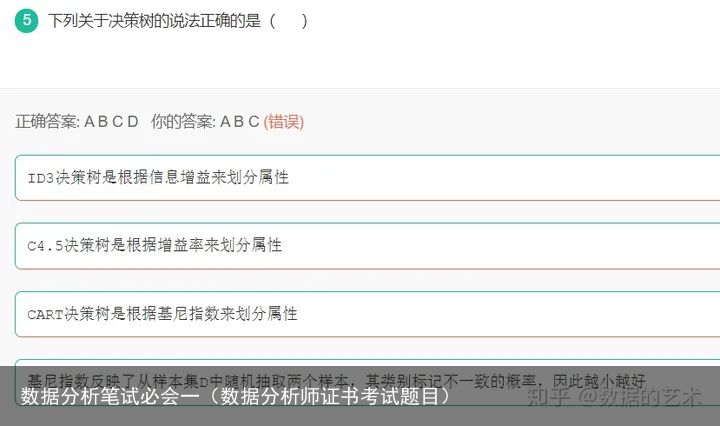
9.划分训练集与测试集的方法

最简单的随机拆分，一般拆为80%训练集20%测试集 或 70%训练集30%测试集。使用训练集训练，然后使用测试集测试模型效果。k折交叉验证：把整个数据集设法均分成k折（一般为随机拆分）。然后使用其中的k-1折进行训练，使用剩下的一折测试。这样实际上训出了k个模型。留一法：k折的极限就是留一。使用m-1个样本进行训练，剩下的那个样本进行测试，简直逗~自助采样法：在原始样本集中有放回的随机采样m次，构成与原始样本集一样大小的训练集（都有m个样本）。根据概率，会有约36.8%的样本没有被采到（另外60+%的样本则有很多被重复采到）。这样可以使用采出来的大小为m且包含重复样本的集合为训练集，剩下约36.8%的样本当测试集。关于验证集的一点补充：之所以把数据集分为训练集和测试集，主要是为了在保证模型不要过拟合的前提下，调整超参数使模型性能尽可能地高。因此一般套路是，在训练集训完，然后在测试集上测试，发现性能掉的厉害或者性能还不够好，调调超参，再训一个试试。因此有种说法：训练集是用来学习超参的。

问题是：虽然模型是在训练集上学的，但超参在测试集的测试结果的反馈下进行调整的，这显然也采到了测试集的信息。这样训出来的模型很有可能结果是，模型表现足够好（性能优秀）且在训练集和测试集上表现一致（看似没有过拟合），但放到新数据集上一看其泛化性能并不好。这是因为模型在整个数据集上其实发生了过拟合。

验证集就是用来解决上述问题的。我们把数据集按622划分为训练集、验证集、测试集。训练一波放到验证集上验证一波，然后调超参，最后觉得差不多了，把模型放到测试集上一测，发现性能没有下降，而在这之前模型和测试集没有发生任何接触，所以证明了其泛化性能，美滋滋，模型训练结束。

10.样本不均衡问题的解决方法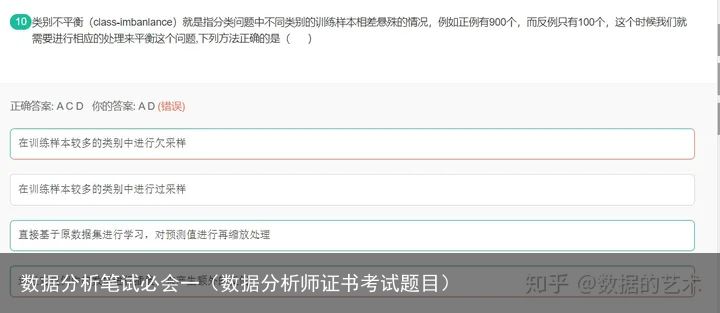

解决类别不平衡问题

欠采样方法

(1)什么是欠采样方法

直接对训练集中多数类样本进行“欠采样”（undersampling），即去除一些多数类中的样本使得正例、反例数目接近，然后再进行学习。

(2)随机欠采样方法

随机欠采样顾名思义即从多数类中随机选择一些样样本组成样本集 。然后将样本集 从 中移除。新的数据集 。

缺点：

随机欠采样方法通过改变多数类样本比例以达到修改样本分布的目的，从而使样本分布较为均衡，但是这也存在一些问题。对于随机欠采样，由于采样的样本集合要少于原来的样本集合，因此会造成一些信息缺失，即将多数类样本删除有可能会导致分类器丢失有关多数类的重要信息。

为了克服随机欠采样方法导致的信息缺失问题，又要保证算法表现出较好的不均衡数据分类性能，出现了欠采样法代表性的算法EasyEnsemble和BalanceCascade算法。