来源 | Data Science from Scratch， Second Edition

作者 | Joel Grus

译者 | cloverErna

校对 | gongyouliu

编辑 | auroral-L

你跟周遭事物的所有联系定义了你是谁。

——亚伦 · 奥康奈尔

当我们面对许多有趣的数据问题时，如果把它们看作由各种类型的节点（node）和连接它们的边（edge）所构成的网络，那就再合适不过了。

例如，你的 Facebook 好友可以看作一个网络中的节点，而连接节点的边可以看作朋友关系。另外一个不太明显的例子是万维网本身，其中的每一个网页都是一个网络节点，而从一个页面到另一个页面的超链接则是这个网络的边。

Facebook 中的朋友关系都是相互的，也就是说，如果我是你的 Facebook 好友，那么你也肯定是我的好友。这样的话，我们就可以说这种网络中的边是无方向的（undirected）。但是，超链接却并非如此，即如果我的网站链接到白宫的网站，并不表示白宫的网站也会链接到我的网站。我们称这种类型的边为有方向的（directed）。

1. 中间性中心度

在第一章中，我们通过计算每个用户所拥有的朋友的数量来计算DataSciencester网络中的关键连接器。现在我们有了足够的工具来看看其他的方法。我们将使用相同的网络，但现在我们将对数据使用命名元组。

回想一下，网络（图22-1）由用户组成：

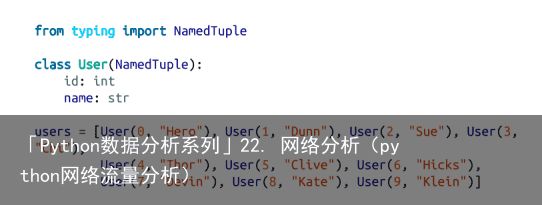
以及朋友关系：

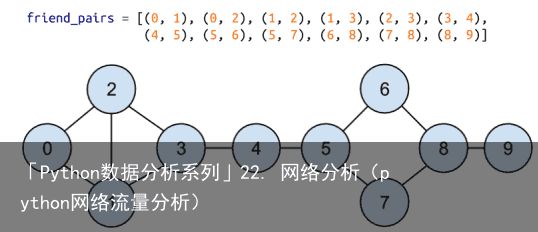图 22-1：DataSciencester 网络

此外，我们还给每个用户的 dict 结构添加了相应的朋友列表：

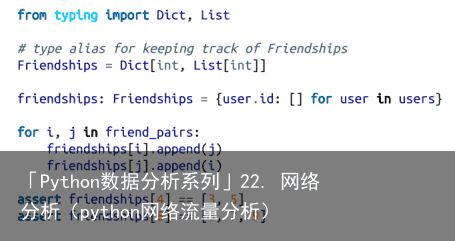
当时，我们对度中心性（degree centrality）的概念不甚满意，因为它与网络中直观展现在我们面前的关键联系人不甚相符。

另一种度量指标是中间性中心度（betweenness centrality），它可以用来找出经常位于其他节点对之间的最短路径中的人。具体而言，中间性中心度可以通过累加经过节点 i 的最短路径与所有两个节点之间的最短路径的比例来求出。

也就是说，如果我们想计算出 Thor 的中间性中心度，首先要计算 Thor 之外的所有用户对之间的最短路径，然后再统计有多少条最短路径通过了 Thor 这个节点。比如说，Chi（id 为 3) 和 Clive（id 为 5) 之间唯一的最短路径经过了 Thor 这个节点，而 Hero（id 为 0) 和 Chi（id 为 3) 之间的两条最短路径则都没有经过 Thor。

因此，作为第一步，我们需要找出所有用户对之间的最短路径。不过，尽管存在许多可以高效计算最短路径的尖端算法，但是按照我们的惯例，这里将采用效率虽低一些但更加容易理解的算法。

这个算法（一个广度优先搜索的实现）在本书中算是比较复杂的一种，所以我们仔细探讨。

1. 我们的目标是建立一个以 from_user 为输入的函数，它能够找出到达其他每个用户的所有最短路径。

2. 我们将通过用户 ID 组成的列表来表示路径。由于每条路径的第一个节点总是 from_ user，因此我们可以在这个列表中将该 ID 忽略。也就是说，这个代表路径的列表的长度等于该路径本身的长度。

3. 我们将维护一个名为 shortest_paths_to 的字典，其键为用户 ID，其值为以该用户 ID 结尾的路径构成的列表。如果最短路径是唯一的，那么这个列表就只包含一个路径。如果有多条最短路径的话，那么该列表将包含所有这些路径。

4. 我们还将维护一个名为 frontier 的队列来存放那些待考察的用户，并且它们的存放顺序就是相应的考察顺序。我们将以用户对的形式——即 (prev_user, user)——来进行存储，这样就能了解我们是如何到达每一个用户的。这个队列是通过 from_user 的所有相邻节点进行初始化的。（当然，我们之前从没有讨论过队列，其实它是专门为“在后端进行插入”操作和“在前端进行删除”操作经过优化的数据结构。在 Python 语言中，队列是由 collections.deque 模块来实现的，实际上它是一种双向队列。）

5. 当我们在图中进行探索的时候，每当发现新的邻居节点，只要还不知道通向它们的最短路径，就将它们添加到队尾以供将来进一步探索，并且以当前用户作为其 prev_user。

6. 当我们把一个用户从队列中删除时，如果之前从未遇到过该用户，那么我们肯定是找到了一个或多个通向它的最短路径：沿着到达 prev_user 的每个最短路径再走一步即是。

7. 当我们从队列中删除一个之前遇到过的用户时，我们不是找到了另一个最短路径（这种情况下我们应该将其添加到队尾），就是找到了一个更长的路径（这种情况下不用将其插入队尾）。

8. 当队列中已经没有用户时，说明我们已经搜遍了整个图（或者至少也是起始用户所能够达到的部分），这时我们就可以停止了。

我们可以将这些步骤放入一个（大型）函数中，代码如下所示：

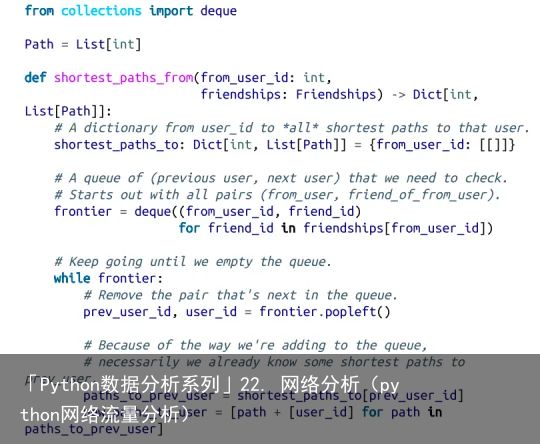
现在，让我们计算一下所有的最短路径：

好了，现在终于可以计算中间性中心度了。对于任意一对节点 i 和 j，我们都知道从 i 到 j 有n 条最短路径。然后，对应于每一条这样的最短路径，我们只要给该路径中的每个节点的中心度加 1/n 即可：

如图 21-2 所示，用户 0 和 9 的中心度为 0（因为它们不在其他用户之间的任何一条最短路径上），而用户 3、4 和 5 则都具有较高的中心度（因为它们都位于多条最短路径上）。

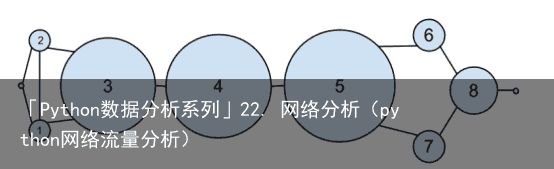图 22-2：根据中间性中心度的大小绘制的 DataSciencester 网络

注意

一般来说，中心度的数值本身并不具有多大意义。我们关心的是每个节点的中心度数值与其他节点的相对大小。

我们可以看到的另一个衡量标准是紧密关系的中心性。首先，我们为每个用户计算她的距离，即她对彼此用户的最短路径长度的总和。由于我们已经计算了每对节点之间的最短路径，因此容易添加它们的长度。（如果有多个最短路径，它们都有相同的长度，所以我们可以只看第一条。）

之后无需计算紧密中心性（图22-3）：

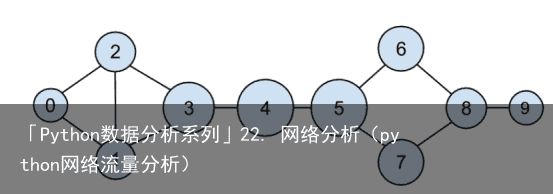图 22-3：根据接近中心度绘制的 DataSciencester 网络

这里的变化要小得多——即使是非常中心的节点也仍然远离外围的节点。

正如我们所看到的那样，计算最短路径是一件苦差事。因此，中间性中心度和接近中心度很少用于大型网络。还有一种不太直观的特征向量中心度（eigenvector centrality），由于计算起来更容易，所以更加常用。

2. 特征向量中心度

要想介绍特征向量中心度，我们就不得不讨论特征向量，而要想讨论特征向量，我们就必须介绍矩阵乘法。

2.1 矩阵乘法

如果A是一个n×m矩阵，B是一个m×k矩阵(注意A的第二维与B的第一维相同)，那么它们的乘积AB是n×k矩阵，其中第(i，j)项是：

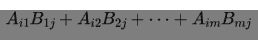
下面，我们仅计算矩阵 A 的第 i 行（可以视为一个向量）与矩阵 B 的第 j 列（也可以视为一个向量）的点积。

我们可以使用第4章中的make_matrix函数来实现这个问题：

如果我们把一个m维向量看作一个(m，1)矩阵，我们可以把它乘以一个(n，m)矩阵来得到一个(n，1)矩阵，然后我们可以把它看作一个n维向量。

这意味着考虑（n，m）矩阵的另一种方法是作为一个线性映射，它将m维向量转换为n维向量：

当 A 是一个方阵时，此操作会将 n 维向量映射为另一个 n 维向量。对于某矩阵 A 和向量v，对向量 v 进行 A 变换有时候会等效于用一个标量来乘向量 v，即所得到的向量与 v 同向。当发生这种情况（且 v 不是零向量）时，我们称 v 为 A 的特征向量。同时，我们称这个乘数为特征值（eigenvalue）。

确定矩阵 A 的特征向量的一种可行方法是取一个随机向量 v，然后利用 matrix_operate 对其进行调整，从而得到一个长度为 1 的向量，重复该过程直到收敛为止：

通过这种构造方法返回的向量 guess 将具备这样的特点：当你对它应用 matrix_operate 函数并将其长度缩为 1 的时候，得到的向量与其自身极为接近。这就意味着它是一个特征向量。

请注意，并不是所有的实数矩阵都具有特征向量和特征值。例如，请看下列矩阵：

上述代码的作用是按照顺时针方向将向量旋转 90 度，这意味着，对于这个矩阵来说，只有一个向量能够映射到自身的数乘上面，这个向量就是零向量。如果你执行 find_ eigenvector(rotate)，它会永远运行下去。即使是具备特征向量的矩阵，有时候也会陷入这种死循环。请看下面的矩阵：

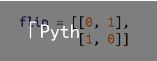
对于任意向量 [x, y]，这个矩阵都会将其映射为 [y, x]。这就意味着，[1, 1] 是一个特征值为 1 的特征向量。但是，如果你从一个 x 和 y 并不相等的随机向量着手的话，那么，find_eigenvector 将会来回交换这两个坐标值，并且永远也不会停下来。（Not-from -scratch 是一个类似于 NumPy 的 Python 库，由于它采用了不同的处理方法，因此能够有效处理这种情形。）尽管如此，只要 find_eigenvector 能返回一个结果，那么这个结果肯定是一个特征向量。

2.2 中心度

该如何利用特征向量来帮助我们理解 DataSciencester 网络呢 ?

首先，我们需要用 adjacency_matrix 来表示网络中的连接，其中第 (i,j) 个元素的值要么为1（如果用户 i 和用户 j 是朋友的话），要么为 0（如果他们不是朋友的话）

对于每个用户来说，他的特征向量中心度就是在 find_eigenvector 返回的特征向量中的该用户对应的那个系数（见图 22-4）：

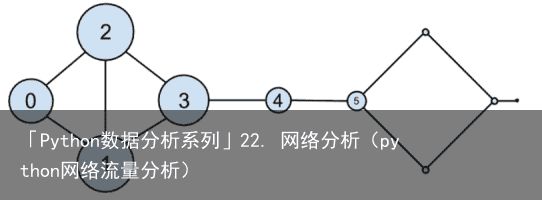图 22-4：根据特征向量中心度绘制的 DataSciencester 网络

注意

由于远远超出本书范围的技术原因，任何非零邻接矩阵都必须有一个特征向量，其所有的值都是非负的。幸运的是，对于这个adjacency_matrix，我们的find_eigenvector函数可以找到它。

特征向量中心度较高的用户，不仅会拥有较多的连接，而且还倾向于连接到具有较高中心度的那些人。

就上图而言，用户 1 和用户 2 具有最高的中心度，这是由于他们两个都有三条连接是通向具有高中心度的对方的。如果我们将其移除，他们的中心度就会直线下降。

在这种小型的网络上中，特征向量中心度的行为会有些怪异。当你尝试增减连接的时候，你会发现，只要对网络进行稍微的修改，中心度的数值就会发生戏剧性的变化。对于比较大型的网络来说，这种情况就不太明显。

我们仍然没有介绍为什么特征向量能够较好地度量中心度。这是因为特征向量意味着，如果你计算：

其结果就等于用一个标量去乘以 eigenvector_centralities，如果你了解矩阵乘法的运算机制，就会知道 matrix_operate 求出的向量的第 i 个元素为：

这实际上就是对连接到用户 i 的各个用户的特征向量中心度进行求和。

换句话说，特征向量中心度就是一个数值，即每个用户对应一个数值，而每个用户的值就是他的相邻值之和的固定倍数。在这种情况下，中心度就意味着要跟处于中心地位的人交朋友。你结交的人的中心度越高，你的中心度也就越高。当然，这明显是一个循环定义，而特征向量就是打破这个循环的突破口。

对此还有另外一种理解方法，那就是考察 find_eigenvector 函数的处理方式。它首先给每个节点随机指定一个中心度，然后重复以下两个步骤，直到这个过程收敛为止。

1. 赋予每个节点一个新的中心度分数，该分数等于该节点相邻节点的（原）中心度分数之和。

2. 将中心向量的向量调整为模为1的向量。

虽然它背后的数学一开始看起来有些不透明，但计算本身相对简单（不像中间中心性），即使是在非常大的图上也很容易执行。（至少，如果使用真实的线性代数库，则很容易在大型图上执行。如果你使用我们的列表实现，你会很困难。）

3. 有向图与PageRank

由于 DataSciencester 没有获得人们的热烈追捧，因此，负责营收的副总决定将网站从交友模式转换为支持模式。事实证明，除了高科技业的猎头非常关心哪些数据科学家备受其他数据科学家推崇之外，没人对科学家之间的好友关系特别在意。

在这个新的模型中，我们所关注的支持 (source, target) 并不表示互反关系，而是表示用户 source 认为用户 target 是一位令人惊畏的数据科学家（见图 22-5）。因此，我们需要考虑这种不对称性：

图 22-5：基于支持关系的 DataSciencester 网络

我们需要解释一下这种不对称性：

之后，我们可以很容易地找到most_endorsed的数据科学家，并将这些信息卖给招聘人员：

然而，“赞同票数”这种指标是很容易被人搞鬼的。实际上，你只要创建大量傀儡账户，然后让这些账户给你投票就行了。或者，你还可以跟朋友们商量好，都彼此捧场也行。（例如用户 0、1 和 2 好像就是这么干的。）

因此，指标最好还要考虑到给你投赞同票的那些人。也就是说，来自得票数较多的人的投票的分量应该重于得票数较少的那些人的投票。这实际上就PageRank 算法的思想精华， Google 就是利用它来给网站排名的，主要考量的就是链接到该网站的其他站点、到达该网站的链接等。（如果这能让你想起特征向量中心性背后的想法，它应该这样做。）下面是这种思想的简化版本。

1.网络中 PageRank 的总分数为 1.0（或 100%）。

2.最初，这个 PageRank 被均匀分布到网络的各个节点中。

3. 在每一步中，每个节点的 PageRank 很大一部分将均匀分布到其外部链接中。

4. 在每个步骤中，每个节点的 PageRank 的其余部分被均匀地分布到所有节点上。

如果我们计算页面排名：

PageRank（见图 22-6）表明，用户 4（也就是 Thor）是排名最高的数据科学家。

图 22-6：利用 PageRank 绘制的 DataSciencester 网络

与用户 0、1 和 2 相比，虽然给他投票的人（2 个）并不多，但是他的得票数还要考虑投票方自身的排名。此外，两个投票方都给只给他投了票，这就意味着他不必与别人分享他们的排名。

4. 延伸学习

• 除了我们使用的中心性概念，还有许多其他的概念（http://en.wikipedia.org/wiki/Centrality）（尽管我们使用的几乎是最流行的）。

• NetworkX（https://networkx.org/）是一个用于网络分析的 Python 库。它为我们提供了许多函数，来帮助计算中心度以及实现图的可视化。

• Gephi（https://gephi.org/）是一个让人爱恨交织的基于图形用户界面的网络可视化工具。