1. 结论：当前中国经济运行存在以下问题：

经过对中国经济微观基础、宏观总量和增长分析可以做出如下判断：

1） 分析期内中国经济保持了较高的增长速度，但未来走向并不乐观，

2） 货币政策失灵，财政政策过度干预导致出现市场被“架空”迹象，

3） 就业中存在赘余，干扰要素配置，

4） 实物资产存量中存在低效产能，或实物资产利用效率偏低，

5） 金融（商业银行）体系内存在流动性陷阱，货币资产向实物资产的转换效率偏低，

6） 家庭部门储蓄率偏高，原因在于未来不确定偏大，狭义的再分配政策和广义的社会政策尚需进一步完善，

解决上述问题，不能仅仅依靠过程政策，设计、重构经济秩序更为重要。中国经济需要更深入、更全面的改革。

根据估计的中国国民经济投入产出关系（不是生产函数！中国国民经济生产不在可能性边界上）。

1）按learning by education测算的人力资本没有产出效果，说明什么？

2）劳动投入的边际产出无法测定，说明有无效劳动投入或过剩就业。

3）TFP自1990年代末至2008年递增，自2010/2011年以后递减。

4）实物资产的边际产出持续递减，2019年边际产出率约30%，资产平均回报（成为资产收入的那部分）率已经低于10%，中间20%的“缺口”到哪里去了？原因何在？

5）基于工资粘性假定可以推出，总供应和物价水平负相关（Phillips曲线就是这样推出来的，中国实情符合Friedman适应性预期假定），原因是物价上升-名义工资有粘性-实际工资下降-劳动力实际成本下降-企业扩大劳动力投入-供应增加；但按之前估计的input-output-relation，中国有过剩就业，扩大供应根本无需增加就业。为什么在有就业过剩的情况下，在中国还能观察到Phillips曲线？那些无效的劳动投入是什么？原因何在？

2. 中国经济投入产出关系的估计-1997-2020

生产函数的估计需要三个变量：不变价GDP，资本存量，劳动力和人力资本。

关于以上变量的具体测算方法参考：

中国宏观经济核算中主要变量的测算方法11 赞同 · 1 评论文章

这里值得注意的是关于人力资本的测算：原始数据测算的结果在2004-2010年间出现先降低后升高的过程，需要进行修正。如下图所示：

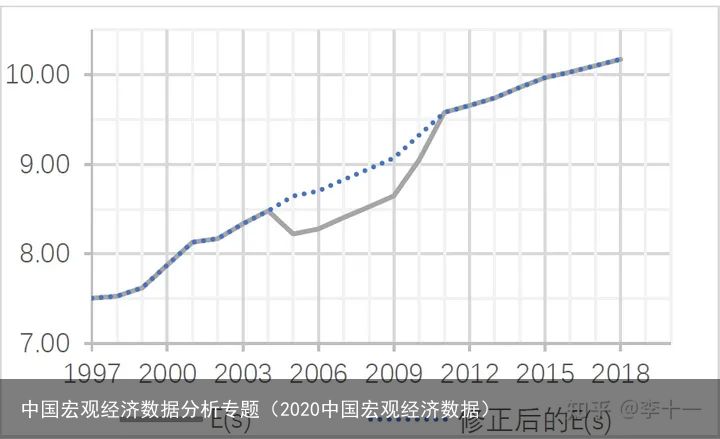1997-2020年平均受教育年限

1. 假设技术水平是不变的投入产出关系符合C-D函数形式:

Y=AKαKLαLY=AK^{\alpha_{K}}L^{\alpha_{L}}

边际技术替代率MRTS等于经济替代率ESR的解特征:

MPKMPL=rw⇒αKAKαK−1LαLαLAKαKLαL−1=rw⇒rw=αKLαLK\frac{MPK}{MPL}=\frac{r}{w} \Rightarrow \frac{\alpha_{K}AK^{\alpha_{K}-1}L^{\alpha_{L}}}{\alpha_{L}AK^{\alpha_{K}}L^{\alpha_{L}-1}}=\frac{r}{w} \Rightarrow \frac{r}{w} =\frac{\alpha_{K}L}{\alpha_{L}K}

⇒KL=αKwαLr\Rightarrow \frac{K}{L} =\frac{\alpha_{K}w}{\alpha_{L}r}

构造计量模型，使用宏观经济数据以上式子进行验证：

KL=αKwαLr+μ\frac{K}{L} =\frac{\alpha_{K}w}{\alpha_{L}r} +\mu

回归结果如表1所示：

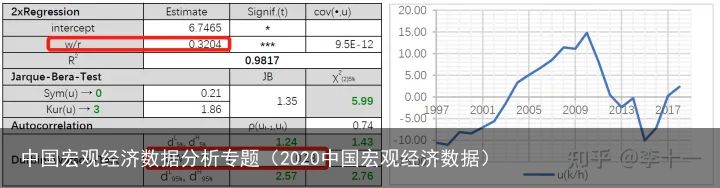表1 回归结果

如上表回归结果所显示的，要素配置除了受要素产出弹性和要素价格影响外，还受到非零截距项（6.7465）的影响。这说明要素配置非最优；虽然模型拟合度高（0.9817），参数估计值也显著，但残差项之间存在序列正相关（DW值为0.28），影响参数估计的有效性。

或者采用对数形式：

ln(KL)=ln(αKαL)+ln(wr)+μ ln( \frac{K}{L} )=ln(\frac{\alpha_{K}}{\alpha_{L}})+ln(\frac{w}{r} ) +\mu

回归结果如表2所示：

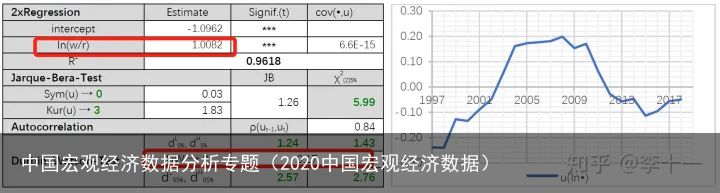表2 回归结果

如上表回归结果所显示的，要素配置除了受要素产出弹性和要素价格影响外，还受到非零截距项（-1.0962）的影响。这说明要素配置非最优；虽然模型拟合度高（0.9618），参数估计值也显著，但残差项之间存在序列正相关（DW值为0.17），影响参数估计的有效性。

值得注意的是，两个回归结果的要素产出弹性比 αK/αL\alpha_{K}/\alpha_{L} 分别为0.3204，0.3341( e−1.0962e^{-1.0962} ).估计结果接近；对数化要素价格比。

结论1：综合以上分析做出判断：从要素投入比 K:LK:L 与要素价格比（平均收入比） w:rw:r 之间的关系看，劳动力 LL 产出弹性 αL\alpha_{L}约为实物资产KK 产出弹性 αK\alpha_{K} 的3倍，但有周期性偏差（残差序列正相关）；残差序列相关虽然影响估计的有效性，由于模型拟合度高，可以认为要素产出弹性比 αK/αL\alpha_{K}/\alpha_{L} 的估计值基本无偏；根据投入侧分析，中国国民经济层面的要素配置在过去二十多年里或近似满足最优条件MRTS=ESR。

进一步的拓展，使用人力资本来对上述回归进行进一步验证：

构造计量模型，使用宏观经济数据以上式子进行验证：

KH=αKwαLr+μ \frac{K}{H} =\frac{\alpha_{K}w}{\alpha_{L}r} +\mu

回归结果如表3所示：

表3 回归结果

或者采用对数形式：

ln(KH)=ln(αKαL)+ln(wr)+μ ln( \frac{K}{H} )=ln(\frac{\alpha_{K}}{\alpha_{L}})+ln(\frac{w}{r} ) +\mu

回归结果如表4所示：

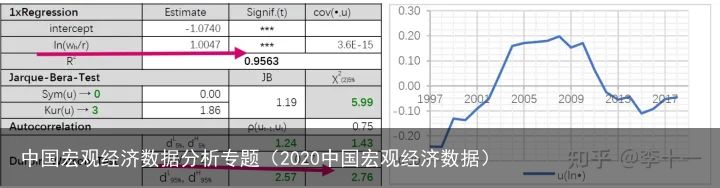表4 回归结果

结论2：比较“劳动力”模型和“人力资本”模型的验证结果可以发现，两者之间没有本质差别，要素产出弹性比 αK/αL\alpha_{K}/\alpha_{L}分别为0.3204，0.3198，0.3341，0.3416。两组模型的估计结果相近，说明在国民经济层面上用人力资本HH 解释要素配置效率与用劳动力 LL 解释要素配置效率，结果无本质差异。该现象值得进一步讨论.

2. 假设技术水平不变，使用人均产出进行估计

lnY=lnA+αKlnK+αHlnH+μlnY=ln A+\alpha_{K}lnK+\alpha_{H}lnH+\mu

⇒lnY−lnL=lnA+αK(lnK−lnL)+αH(lnH−lnL)+μ\Rightarrow lnY-lnL=lnA+\alpha_{K}(lnK-lnL)+\alpha_{H}(lnH-lnL)+\mu

⇒lny=lnA+αKlnk+αHlnh+μ\Rightarrow lny=lnA+\alpha_{K}lnk+\alpha_{H}lnh+\mu

回归结果如表5所示：

表5 回归结果

结论3：回归结果显示人力资本产出弹性显著为负（-1.3697），即：人力资本积累与国民经济产出显著负相关，这一结果显然有悖于常理。正常情况下，人力资本积累可以没有产出效果，但不应该干扰生产。由此可以推断：现行教育体制内的人力资本积累对中国国民经济生产没有显著贡献；技术进步不变的模型不适合用于描述中国国民经济投入产出关系。

3. 假设技术水平变化的投入产出关系符合C-D函数形式:

Y=A(H,K)KαKLαLY=A\left( H,K\right)K^{\alpha_{K}}L^{\alpha_{L}}

需要说明的是：技术进步源自：干中学（learn by doing）是源自资本品的积累；人力资本积累(learn by education)源自劳动力所获得教育；由于资本品本身包含了一定的技术进步，并且工人在使用过程中的技术和效率的提升都难以测量。关于技术进步方向的问题，目前还没有足够的经验证据是偏向资本还是劳动力。

构造计量模型，使用宏观经济数据以上式子进行验证：

lnY=lnA(H,K)+αKlnK+αLlnL+μlnY=lnA(H,K)+\alpha_{K}lnK+\alpha_{L}lnL+\mu

回归结果如表6所示：

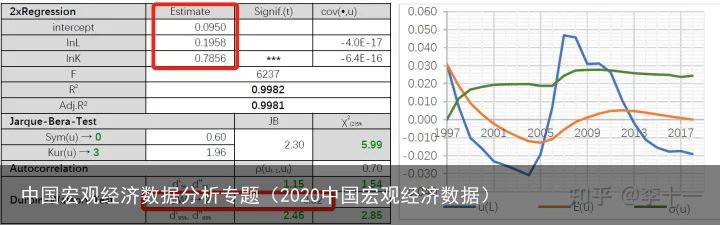表6 回归结果

回归结果显示：

1）lnA(H,K)lnA(H,K) （intercept）不显著，可能是一个变量；

2）劳动力 LL 的产出弹性 αL\alpha_{L} 不显著，或因 αL\alpha_{L} 为非常量，或因 lnLlnL 和 lnKlnK 之间存在共线性；

3）模型拟合度高，F值大，说明与现实相符；

4）残差项之间序列正相关（DW=0.32）。

或者使用人力资本 HH 与实物资产 KK 组合的投入产出回归模型,

lnY=lnA(K)+αKlnK+αHlnH+μlnY=lnA(K)+\alpha_{K}lnK+\alpha_{H}lnH+\mu

回归结果如表7所示：

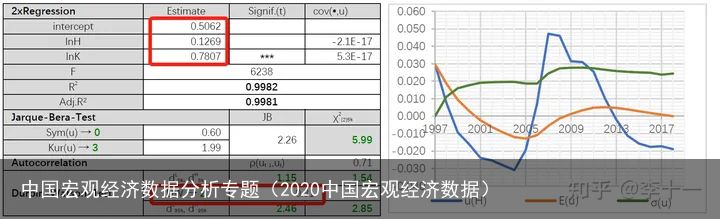表7 回归结果

比较两个回归结果发现：采用人力资本 HH 替代劳动力 LL，回归结果无本质差异。原因或是人力资本积累没有明显的产出效果！此外，在HH 和 LL 之间同样存在共线性问题。

由于 回归模型中的残差项序列正相关，所以对其做进一步分析（residual analysis）。将残差序列 μ\mu与实物资产存量KK 、就业规模 LL 和人力资本存量 HH 的增长率 gKg_{K} 、 gLg_{L} 和 gHg_{H} 作比较后发现，实物资产积累可能对 μ\mu 有影响：以2008/2009年为界，之前的 μ\mu随实物资产积累呈上升态，之后随实物资产积累呈下降态。

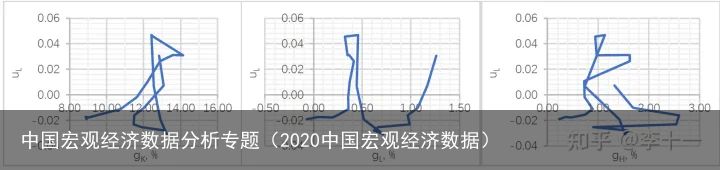
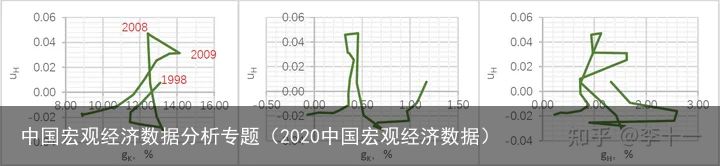
结论4：回归模型中的 μ\mu 是一个非随机变量，包含了 lnAlnA 中可能和实物资产积累有关的一个分量，需要做内生化处理。因此，设 lnA=A(K)lnA=A(K) ，其数值为式中截距项与残差项之和：

A^=elnA+μ=elnY−αKlnK−αHlnH\hat A=e^{lnA+\mu}=e^{lnY-\alpha_{K}lnK-\alpha_{H}lnH}

求解出的全要素生产率如图所示：

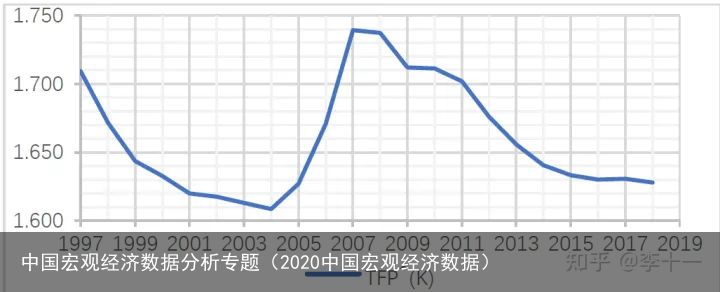图1 全要素生产率变化情况

假设全要素生产率的函数形式如下所示：这里技术进步既包含了资本偏向技术进步，也包含了人力资本偏向型技术进步。

A=exp(μ1(Kt⁄Kt0)γ+μ2(Ht⁄H0)ν)A=exp(μ_1 (K_t⁄K_{t_0 } )^γ+μ_2 (H_t⁄H_0 )^ν )

这里，K0K_0是基期的资本存量，H0H_0是基期的人力资本存量，参数γγ和νν分别表示资本规模效应和人力资本规模效应。

基于前文分析结论，考虑到人力资本效果并不显著，假设技术进步如下所示：

A^=α+β1eKtKt0−1+μ\hat A=\alpha+\beta_{1}e^{\frac{K_t}{K_{t_0 }}-1}+\mu

这里需要说明的是，1997-2020年间中国经济一直处于不断改革和优化的阶段，技术进步受到各种外在的冲击，既有资本深化带来的，也有外部冲击造成的波动，因此需要加入时间哑变量剔除掉一些波动冲击。因此假设技术进步如下所示：

A^=α+β1D97−08eKtK97−1+β2D97−08+β3D12−20(KtK97−1)+μ\hat A=\alpha+\beta_{1}D_{97-08}e^{\frac{K_t}{K_{97}}-1}+\beta_{2}D_{97-08}+\beta_{3}D_{12-20}({\frac{K_t}{K_{97}}-1} )+\mu

D97−08={1,1997−20080,otherwise\begin{align*} \begin{split} D_{97-08}= \left \{ \begin{array}{ll} 1, & 1997-2008\\ 0, & otherwise \end{array} \right. \end{split} \end{align*} ;D12−20={1,2012−20200,otherwise\begin{align*} \begin{split} D_{12-20}= \left \{ \begin{array}{ll} 1, & 2012-2020\\ 0, & otherwise \end{array} \right. \end{split} \end{align*}

回归结果表8所示：

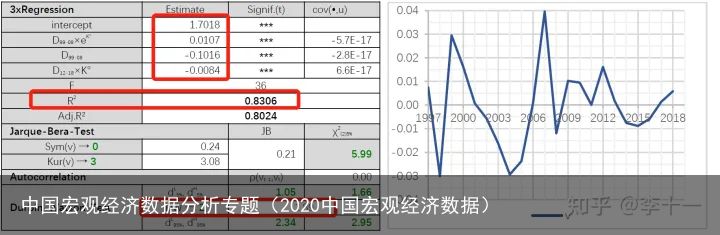表8 回归结果

回归分析显示，拟合度只有83.06%略偏低，但其他指标均令人满意。拟合度偏低的原因可能是忽略了偶发性冲击（ad-hoc impacts），如1997/1998年的亚洲金融危机，1999/2000年生产者对中国加入WTO后的利好预期，2007年房地产行业升温对产能利用的激励; 2015年开始的供给侧改革等。基于以上考虑，对以上模型进行如下补充：

A^=α+β1D97−08eKtK97−1+β2D97−08+β3D12−20(KtK97−1)+β4impactad−hoc+μ\hat A=\alpha+\beta_{1}D_{97-08}e^{\frac{K_t}{K_{97}}-1}+\beta_{2}D_{97-08}+\beta_{3}D_{12-20}({\frac{K_t}{K_{97}}-1} )+\beta_{4}impact_{ad-hoc}+\mu

D97−08={1,1997−20080,otherwise\begin{align*} \begin{split} D_{97-08}= \left \{ \begin{array}{ll} 1, & 1997-2008\\ 0, & otherwise \end{array} \right. \end{split} \end{align*} ;D12−20={1,2012−20200,otherwise\begin{align*} \begin{split} D_{12-20}= \left \{ \begin{array}{ll} 1, & 2012-2020\\ 0, & otherwise \end{array} \right. \end{split} \end{align*}; Impactad−hoc={1,1998;1999;2000;2007;20160,otherwise\begin{align*} \begin{split} Impact_{ad-hoc}= \left \{ \begin{array}{ll} 1, & 1998;1999;2000;2007;2016\\ 0, & otherwise \end{array} \right. \end{split} \end{align*}

回归结果表9所示：

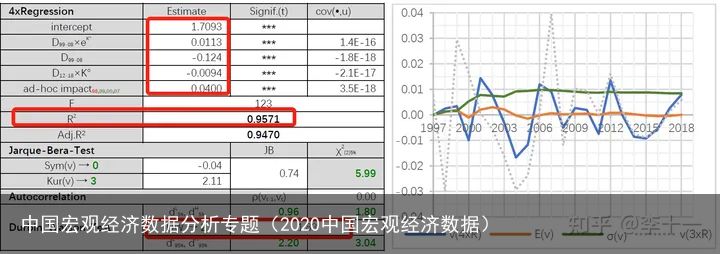表9 回归结果

结论5：修正后的模型拟合度明显提高，模型的无偏性有所改善（Sym(v)=-0.04）。同时，对模型的修正没有影响残差项随机分布的特点（见JB检验和DW检验结果）。这说明，以上技术进步的设定基本再现了过去二十多年中国国民经济全要素生产率变化的规律。

使用估计的内生技术进步对投入产出关系进行估计：

lnY=lnA^+αKlnK+αHlnH+μlnY=ln\hat A+\alpha_{K}lnK+\alpha_{H}lnH+\mu

回归结果如表10所示：

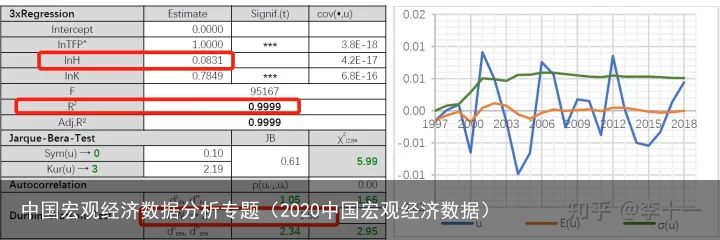表10 回归结果

上表中，其他回归指标均好，但人力资本 HH的产出弹性依然不显著。为了排除多重共线性可能带来的干扰，对式做如下变形：

lnY=lnA^+αKlnK+αHlnH+μlnY=ln\hat A+\alpha_{K}lnK+\alpha_{H}lnH+\mu

⇒gY=gA+αKgK+αHgH+μ\Rightarrow g_Y=g_A+\alpha_{K}g_K+\alpha_{H}g_{H}+\mu

回归结果如表11所示：

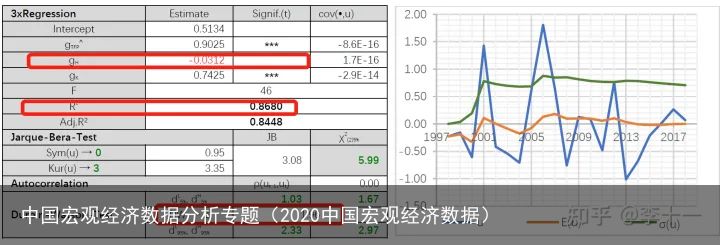表11 回归结果

结论6：但是对变形式子的回归结果显示，人力资本 HH的产出弹性αH\alpha_{H} 不但没有变得显著，反而成为了负数。由此可以断定，在中国国民经济生产中存在劳动力和人力资本过剩现象，增加就业或人力资本积累不产生边际产出效果！

4. 中国1997-2020投入产出关系如下所示:

Y=A(H,K)KαKLαLY=A\left( H,K\right)K^{\alpha_{K}}L^{\alpha_{L}}

A^=α+β1D97−08eKtK97−1+β2D97−08+β3D12−20(KtK97−1)+β4impactad−hoc+μ\hat A=\alpha+\beta_{1}D_{97-08}e^{\frac{K_t}{K_{97}}-1}+\beta_{2}D_{97-08}+\beta_{3}D_{12-20}({\frac{K_t}{K_{97}}-1} )+\beta_{4}impact_{ad-hoc}+\mu

D97−08={1,1997−20080,otherwise\begin{align*} \begin{split} D_{97-08}= \left \{ \begin{array}{ll} 1, & 1997-2008\\ 0, & otherwise \end{array} \right. \end{split} \end{align*} ;D12−20={1,2012−20200,otherwise\begin{align*} \begin{split} D_{12-20}= \left \{ \begin{array}{ll} 1, & 2012-2020\\ 0, & otherwise \end{array} \right. \end{split} \end{align*}; Impactad−hoc={1,1998;1999;2000;2007;20160,otherwise\begin{align*} \begin{split} Impact_{ad-hoc}= \left \{ \begin{array}{ll} 1, & 1998;1999;2000;2007;2016\\ 0, & otherwise \end{array} \right. \end{split} \end{align*}

回归结果表12所示：

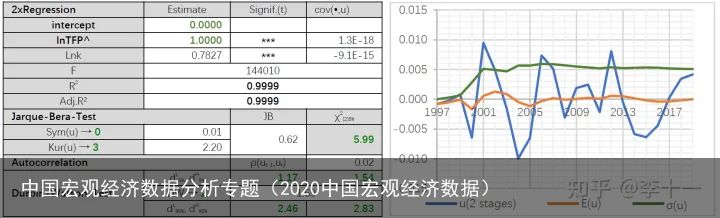表12 回归结果

结论7： 基于以上结果可以得到，1997-2020年间中国投入产出关系表达式如下：

Y^=e0.999ln(1.014+0.007D97−08eKtK97−1−0.075D97−08−0.005D12−20(KtK97−1)+0.024Impactad−hoc)K0.783L0.217\hat Y=e^{0.999ln(1.014+0.007D_{97-08}e^{\frac{K_t}{K_{97}}-1}-0.075D_{97-08}-0.005D_{12-20}({\frac{K_t}{K_{97}}-1} )+0.024Impact_{ad-hoc})}K^{0.783}L^{0.217}

D97−08={1,1997−20080,otherwise\begin{align*} \begin{split} D_{97-08}= \left \{ \begin{array}{ll} 1, & 1997-2008\\ 0, & otherwise \end{array} \right. \end{split} \end{align*} ;D12−20={1,2012−20200,otherwise\begin{align*} \begin{split} D_{12-20}= \left \{ \begin{array}{ll} 1, & 2012-2020\\ 0, & otherwise \end{array} \right. \end{split} \end{align*}; Impactad−hoc={1,1998;1999;2000;2007;20160,otherwise\begin{align*} \begin{split} Impact_{ad-hoc}= \left \{ \begin{array}{ll} 1, & 1998;1999;2000;2007;2016\\ 0, & otherwise \end{array} \right. \end{split} \end{align*}

基于以上估计的投入产出关系，可以得到GDP估计值和TFP估计量如下图所示：

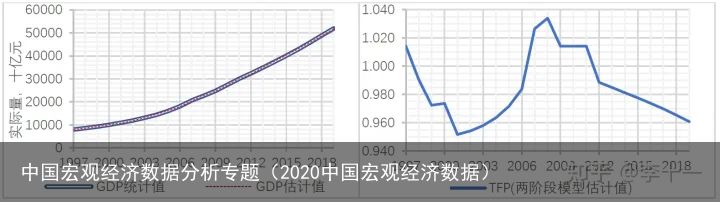图2：GDP估计值和TFP测算值

由上图可以得到：其中，GDP估计值与现实的最大偏差为1.001%，平均偏差为0.416%； TFP测算值在2008年最高，达到1.034；2019年的TFP测算量相当于2008年水平的92.9%。一个解释是：美国次贷危机引起全球经济危机后，中国不再是FDI的目标国，因此imitation不行，要innovation。没有FDI，spillovers的效果也就消失。

进一步拓展分析：对估计的投入产出关系求偏导数算得实物资产的边际产出，将其与按收入统计测算的资本平均收益率对比，发现两者之间存在明显差异。

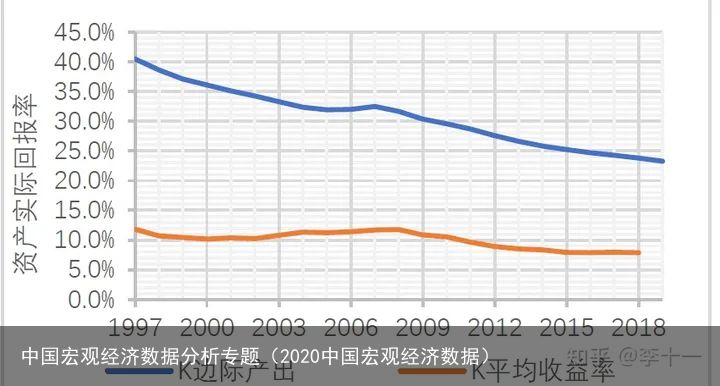图3：边际产出和平均收益率

结论8：实物资产平均收益率和边际产出之间的缺口意味着在资本积累过程中存在“损耗”，导致实物资产使用者实际承担的单位成本r2高于资本市场的平均回报率r1。实物资产的边际产出持续递减，2019年边际产出率约30%，资产平均回报（成为资产收入的那部分）率已经低于10%，中间20%的“缺口”到哪里去了？原因何在？

3. 中国家庭部门消费函数估计-1997-2020

1.基于绝对消费理论和消费者效用函数，

设定一下估计模型：

lnc=\alpha+\beta_{1}lnY_{I}+\beta_{2}lnP+\mu

回归结果如表13所示：

表13 回归结果

以上回归结果验证了绝对消费理论和效用函数理论，然而回归结果的残差具有序列相关性，需要进一步的分析。使用差分回归模型进行分析：

\Delta c=\alpha+\beta_{1}\Delta Y_{I}+\beta_{2}\Delta P+\mu

回归结果如表14所示：

表14 回归结果

结论9：

√ 收入对消费决策有显著（正）影响；

√ 价格对消费决策有显著（负）影响（替代效果+收入效果）；

x 残差序列正相关（DW=1.08），原因可能在于计量模型中遗漏关键的解释变量。

进一步分析，拓展

2. 基于绝对消费理论和消费者效用函数+消费多样组合的福利和收入效果-单周期

数理模型推论（hypothesis）

- 收入上升不仅可以满足更高的消费支出，也能使消费选择和消费品组合可能性变大；

- 消费品多样组合会带来价格指数效果和福利效果；

- 高收入家庭的消费选择可能性大，从消费品多样组合的价格指数效果和福利效果中获益也大，其消费倾向较低收入家庭相对低；

→ 收入分配会影响家庭的消费倾向。

图4，收入分配变化趋势

设定一下估计模型：

lnc=\alpha+\beta_{1}lnY_{I}+\beta_{2}lnP+\beta_{3}D_{97-08}+\beta_{4}D_{97-08}*lnY_{I}+\mu

\begin{align*} \begin{split} D_{97-08}= \left \{ \begin{array}{ll} 1, & 1997-2008\\ 0, & otherwise \end{array} \right. \end{split} \end{align*}

回归结果如表15所示：

表15 回归结果

进一步使用差分理论进行验证：

\Delta c=\alpha+\beta_{1}\Delta Y_{I}+\beta_{2}\Delta P+\beta_{3}\Delta \frac{Y_K}{Y_L}+\mu

回归结果如表16所示：

表16 回归结果

结论10：以上回归结果显示： \Delta Y_K/Y_L 对 \Delta c的影响不显著，原因或与2014至2016年的股市（预期货币性资产回报上升→多周期消费和储蓄计划）和楼市（预期财产性消费品价格上升→Pigou效应）有关。

进一步修正模型：

\Delta c=\alpha+\beta_{1}\Delta Y_{I}+\beta_{2}\Delta P+\beta_{3}\Delta \frac{Y_K}{Y_L}+\beta_{4}D_{14-16}+\beta_{5}D_{14-16}*\Delta Y_{I}+\mu

\begin{align*} \begin{split} D_{14-16}= \left \{ \begin{array}{ll} 1, & 2014-2016\\ 0, & otherwise \end{array} \right. \end{split} \end{align*}

回归结果如表17所示：

表17 回归结果

3. 基于绝对消费理论和消费者效用函数+消费多样组合的福利和收入效果-两周期动态模型分析

考虑到1997-2020年间，中国存贷款利率基本上是固定的常数，一次利率对消费的影响可以近似认为是常数，因此设定一下估计模型：

lnc_{t+1}=\alpha+\beta_{1}lnc_{t}+\beta_{2}lnp_{t+1}+\mu

回归结果如表18所示：

表18 回归结果

回归结果显示：

√ 上一期消费对当前消费决策有显著（正）影响；

√ 价格对消费决策有显著（负）影响（替代效果+收入效果）；

x 残差序列正相关（DW=0.79），原因可能在于计量模型中遗漏关键的解释变量。

进一步分析，拓展 鉴于 t+1 期的价格 p_{t+1} 在 t期尚未知，利用适用性预期（adaptive expectation）、并考虑信息损失（熵值衰退→对数转换），用式一下式子近似：

E\left( p_{t+1}\right)=p_{0}ln\left( p_{t} \right)

基于以上近似可以得到拓展的积累模型：

lnc_{t+1}=\alpha+\beta_{1}lnc_{t}+\beta_{2}ln(lnp_{t})+\mu

回归结果如表19所示：

表19：回归结果

从以上回归结果的残差项可以看出，价格对消费计划的调节以1997/1998年为界前后有区别。中国全面放开物价管制、引入市场机制始于1993/1994年，以后若干年市场渐趋成熟，政府协调供需、平衡计划的功能逐步被市场取代，价格预期对消费行为产生影响。

进一步使用差分理论进行验证：

\Delta c_{t+1}=\alpha+\beta_{1}\Delta c_{t}+\beta_{2}lnp_{t}+\mu

回归结果如表20所示：

表20 回归结果

结论11：基于以上回归分析可以看到，跨期消费行为具有连续性，说明家庭倾向于平滑消费路径。这种倾向可以用风险厌恶（risk aversion）或棘轮效应（ratcheting effect, a la Duesenberry）来解释。价格预期对消费计划有调节作用，但拓展模型中价格预期对消费计划的影响与Pigou效应相悖，有待进一步讨论。此外，模型中的残差项在2007年以后波动性增大，或与收入分配有关，需要进一步验证。

• 验证结论

市场机制自上世纪90年代中后期起对调节消费计划产生影响；

在中国家庭部门的消费路径上可以观察到风险厌恶倾向和Pigou效应；

准动态分析中可能忽略了的关键的解释变量。

4. 基于绝对消费理论和消费者效用函数-两周期动态模型分析-修正模型

消费受到以下因素的影响：

时间偏好对消费计划的影响：利率对消费计划的影响（a la Fischer）：价格预期对消费计划的影响（a la Pigou）：收入对消费计划的影响（a la Keynes）：

基于以上考虑，修正模型设定如下：

lnc_{t+1}=\alpha+\beta_{1}lny_{t}+\beta_{2}ln(lnp_{t})+\mu

回归结果如表21所示：

表21 回归结果

以2008/2009年为界，拓展回归模型的残差项序列走向分别呈下行和上行趋势，或与收入分配有关。进一步对拓展模型进行修正：

lnc_{t+1}=\alpha+\beta_{1}D_{97-08}+\beta_{2}lny_{t}+\beta_{3}lny_{t}*D_{97-08}+\beta_{4}ln(lnp_{t})+\mu

\begin{align*} \begin{split} D_{97-08}= \left \{ \begin{array}{ll} 1, & 1997-2008\\ 0, & otherwise \end{array} \right. \end{split} \end{align*}

回归结果如表22所示：

表22：回归结果

结论12：比较单周期模型和两周期模型可以看出，无需考虑预期或预期与现实相吻合（→理性预期，rational expectation）；两周期模型，模型中含适应性预期（adaptive expectation）。从模型（与现实）的拟合度看，理性预期模型和适应性预期模型均可用于分析家庭部门的消费行为，结果无本质差异。对此的解释是：日常消费可以随着决策环境的变化连续调整，因此适应性预期近似等同于理性预期。

5. 基于绝对消费理论和消费者效用函数-多周期动态模型分析

消费决策 c_{t}受到以下因素的影响：

若预期消费价格 p_{t} 上升，则计划未来的消费（相对当前）减少（a la Pigou）， 若预期利率 r_{t}上升，则计划未来的消费（相对当前）增加（a la Fischer），若对消费和休闲的当前偏好\eta 增加，则计划未来的消费（相对当前）减少；

基于动态优化求解可以得到：

休闲决策 l_{t} 的动态方程如下所示：

g_{l_{t}}=\frac{\dot l_{t}}{l_{t}}=\frac{r_{t}-g_{w_{t}}-\eta}{\varepsilon_{l}}

消费决策 c_{t} 的动态方程如下所示：

g_{c_{t}}=\frac{\dot c_{t}}{c_{t}}=\frac{r_{t}-g_{p_{t}}-\eta}{\varepsilon_{c}}

专业化分工和大规模协作生产要求对个体工作时间以及节奏制定规范。因此现代社会中的工作时间和退休年龄是以牺牲个体自由为代价、不可任意连续调节的外生制度变量（异化 – Entfremdung a la Marx），即l_{t} 给定，此时， g_{l_{t}}=0 。

g_{l_{t}}=\frac{\dot l_{t}}{l_{t}}=\frac{r_{t}-g_{w_{t}}-\eta}{\varepsilon_{l}}=0

\Rightarrow \eta= r_{t}-g_{w_{t}}

推论1：家庭会根据利率和工资率变化调整其效用评价贴现率\eta ，以适应制度环境。 从长期看，利率 r_{t} 既不持续递增、亦不持续递减；工资率 w_{t} 则持续上升。随着劳动生产率提高，家庭对当前消费和休闲的偏好相应递减，计划更具前瞻性.

代入以上式子到消费的动态方程，可以得到：

g_{c_{t}}=\frac{\dot c_{t}}{c_{t}}=\frac{g_{w_{t}}-g_{p_{t}}}{\varepsilon_{c}}=\frac{g_{\omega_{t}}}{\varepsilon_{c}}

上式中， \omega 为实际工资率（在名义量中除物价因素）。

由于风险厌恶型家庭的跨期效用替代弹性 0">\varepsilon_{c}>0，因此其计划消费增长率g_{c_{t}} ：

与预期收入增长率正相关（→Keynes的绝对收入理论）， 与预期物价增长率 g_{p_{t}} 负相关（→Pigou效应）。

以上推测与之前经验验证的结论吻合。

然而，描述家庭消费决策的计量模型时采用g_{c_{t}}=\frac{g_{w_{t}}-g_{p_{t}}}{\varepsilon_{c}}回归结果并不理想。原因之一是解释变量之间存在共线性（collineality）。

g_{w_{t}} 和 g_{p_{t}} 之间的同向变化限制了 g_{c_{t}}大幅波动，符合风险厌恶型家庭的偏好特点。由此推测，若家庭部门整体厌恶风险，则经济系统具有避免名义收入水平和物价水平相背变化的自适应能力.

尽管收入和物价同向变化符合经济学逻辑，但是在线性回归模型中需要避免解释变量之间存在共线性。对策之一是直接采用实际工资增长率 g_{\omega_{t}} 解释消费增长率 g_{c_{t}} 。三者的时间序列相似，两两正相关，但拟合度却偏低。如表23 所示：

表23 回归结果

拟合度偏低的原因可能在于以下三方面：

1）回归模型适用于再现单个家庭的消费行为。在宏观层面上， L_{t}体现家庭部门的整体就业规模，劳动收入增长率既取决于工资增长率，也取决于就业增长率;

2) 模型中设定 \eta 随 r_{t} 和 g_{w_{t}} 变化而即时调整或与现实不尽相符。但如果 \eta为常数，则模型的拟合度低（R2=6.47%），且残差项\mu 与 g_{w_{t}} 以及正相关；

3）静态和准动态模型显示：收入分配对家庭消费有显著影响。此外，1993/1994年的物价改革，1997/1998年的社保改革和2014至2016年的股价波动（影响货币性资产积累）以及楼价波动（影响财产性消费）都可能影响家庭的消费行为。

基于以上考虑，对回归模型进行修正，实际消费修正模型如下所示：

g_{c_{t}}=\alpha+\beta_{1}g_{y_{lt}}+\beta_{2}D_{95}+\beta_{3}D_{99-20}+\beta_{4}D_{97-08}+\mu

\begin{align*} \begin{split} D_{95}= \left \{ \begin{array}{ll} 1, & 1995\\ 0, & otherwise \end{array} \right. \end{split} \end{align*} ;\begin{align*} \begin{split} D_{99-00}= \left \{ \begin{array}{ll} 1, & 1999-2000\\ 0, & otherwise \end{array} \right. \end{split} \end{align*}; \begin{align*} \begin{split} D_{97-08}= \left \{ \begin{array}{ll} 1, & 1997-2008\\ 0, & otherwise \end{array} \right. \end{split} \end{align*}

回归结果如表24所示：

表24 回归结果

回归结果中：

Dummy1用于修正1994年工资因物价改革大幅上调后对实际消费的滞后影响；Dummy2用于修正1997/1998年社保体制改革对消费行为“先抑后扬”的影响； Dummy3用于修正收入分配变化对实际消费的影响。

基于以上考虑，对回归模型进行修正，名义消费修正模型如下所示：

g_{c_{t}}=\alpha+\beta_{1}g_{y_{lt}}+\beta_{2}g_{p_{t}}+\mu

回归结果如表25所示：

表25 回归结果

回归结果显示：上表中 g_{y_{lt}} 的系数为35.5%， 1">\varepsilon_{c}>1。这说明中国家庭具有明显的风险厌恶倾向。

由于回归结果中的残差项可能序列正相关（DW值为1.51），对名义消费模型做出如下修正：

g_{c_{t}}=\alpha+\beta_{1}g_{y_{lt}}+\beta_{2}g_{p_{t}}+\beta_{3}D_{95}+\beta_{4}D_{99-20}+\beta_{5}D_{97-08}+\mu

\begin{align*} \begin{split} D_{95}= \left \{ \begin{array}{ll} 1, & 1995\\ 0, & otherwise \end{array} \right. \end{split} \end{align*} ;\begin{align*} \begin{split} D_{99-00}= \left \{ \begin{array}{ll} 1, & 1999-2000\\ 0, & otherwise \end{array} \right. \end{split} \end{align*}; \begin{align*} \begin{split} D_{97-08}= \left \{ \begin{array}{ll} 1, & 1997-2008\\ 0, & otherwise \end{array} \right. \end{split} \end{align*}

回归结果如表26所示：

表26 回归结果

模型修正后，回归结果令人满意； g_{y_{lt}} 估计值小于1，在0.1%的水平上显著，证实了中国家庭部门整体具有厌恶风险的倾向。

结论13：

修正的实际和名义消费回归模型均显示，实际劳动收入增长g_{y_{lt}} 对实际消费增长 g_{c_{t}} 和名义消费支出增长 g_{c_{t}} 有显著影响， g_{y_{lt}} 对 g_{c_{t}} 的贡献率约为0.52；跨期效用替代弹性估计值的置信区间窄 \varepsilon_{c}（近似为常数），且大于1，即中国居民有明显的风险厌恶倾向。根据风险厌恶倾向推测，中国家庭高储蓄、低消费行为与未来不确定性支出有关，如子女教育、自身养老和家庭医疗保健等大额支出。

从数理模型推得：影响家庭消费决策的主要因素是劳动收入，资产收入对家庭消费没有直接影响，而是通过收支预算家庭决策约束。上述推论的前提是：劳动时间 L_{t} 为外生制度性变量，家庭对效用评价的时序偏好 \eta - 随利率 r_{t} 和名义工资增长率 g_{w_{t}} 变化而调整。经验分析的结果显示，上述假定和推论与中国现实相符。

根据回归分析结果，价格上涨率 g_{p_{t}} 对同期名义消费支出增长率 g_{c_{t}} 的影响系数大于1。由于物价上升会引起名义消费支出1:1上升，而预期价格上升会引起财产性消费提前。因此，若Pigou（财产性消费）效应明显，则价格上涨率 g_{p_{t}}对同期名义消费支出增长率g_{c_{t}} 的影响系数应小于1。据此推测，Pigou效应在中国家庭部门整体消费行为中的体现不明显，中国居民在积累资产时或许更看重货币性资产。

针对家庭部门构建的动态优化模型隐含理性预期机制，理由是：消费决策往往即时产生效果，后继影响的时滞短；通过连续修正（适应性）预期，决策者能够按经济环境的实际变化（近似于理性预期）及时调整其决策。基于理性预期的家庭部门动态优化数理模型在经验分析中得到了验证。

4. 投资行为

1.结论

从以上的经验分析中可知：

∆ _ = \alpha+ \beta_1 P_{t-1} +\beta_2 \Delta P_{t} +\beta_3 + \beta_4g_{r_{Q}}+\varepsilon

投资变化 ΔI 与预期价格水平变化正相关，与企业部门投资当期实物资产边际产出（或投资当期物价水平变化）正向关；平均融资成本 r_{Q} 的变化和平均资产收益率 r_{s}的变化均对投资I的变化没有显著影响，原因或在于大部分企业经营者（代理人 agent，而非所有者和委托人 principal）对资产收益并不十分关注；真正约束投资的可能并非融资成本，而是某些非货币性约束，而且可能有较大的不确定性，不易预期；

综合经验分析的结果，即企业部门投资行为：

受价格预期和当期实物资产边际产出的影响，不受融资条件以及资产收益的的影响可以初步推断：企业部门的投资似有短期行为倾向；企业经营者追求短期盈利、而非（长期）财产最大化；投资受到过程性政策影响，经常性的过程干预使得长期投资规划无实际意义；融投资环境不确定，影响企业经营者的时间偏好，导致短期行为。•中国经济处在向资本密集型转变（产业结构和城市化演变）的过程中（lnK 与 lnGDP 正向关， ΔlnP 之所以对 lnK 有负影响是因为 GDP 为名义量，含价格因素）；实物资产积累导致其边际产出下降，亟需用技术进步来弥补；金融服务效率（体现在 r_{Q} 上）虽然对投资增量 ΔI 没有显著影响，但对实物资产存量 K ― 投资积累的结果 ― 有显著负影响；从长期看，金融“不便利”制约了实体经济规模扩张，如何提高金融服务效率也是中国亟需解决的问题。

5. 金融中介

当前中国经济运行中存在，实物资产边际产出和资本平均收益率之间存在明显差异。这一差异不能简单解释为“损耗”，而是收入的一部分，其流向需要进一步讨论。

在宏观经济模型中，一般假定家庭部门的储蓄S等同于企业部门的（净）投资I ，即：在货币性资产（对应于 \dot K=S ）向实物资产（对应于 \dot K=I ）转换时无“损耗”。

现实中，货币性资产向实物财产的转换 ― 即在从家庭部门的储蓄 S到企业部门筹措资金、购置固定资产I 、完成实物资产积累 \dot K 的过程中，需要金融中介提供融资便利 Q ：

图4 资本流动图

上图中，企业资产为家庭部门或国家所有。金融企业和非金融企业的盈余以分红、股息等形式支付给资产所有者，构成收入的一部分 ― 除劳动收入以外的财产收入，再通过储蓄影响资产积累。

金融中介在向企业提供融资便利时会收取高于存款利率 r_{s} 的费用 r_{q} 。如果金融中介效率高，则 l_{q} 相对少， r_{q} 与 r_{s} 的差距相应较小；反之，则融资便利收费 r_{q}*q 中的较多部分会作为劳动报酬 w*l_{q} 支付给金融中介雇佣的员工， r_{q} 与 r_{s}的差距扩大。实物资产边际产出和资本平均收益率之间的差异即金融中介的劳动力成本w*l_{q} ，体现金融效率.

图5 金融效率

从金融费率在实物资产边际产出中的占比来看，中国金融业的效率偏低。原因何在？

中国的金融业由少数超大银行（5大国有股份制银行的信贷市场占有率在四成以上）和众多中小银行以及其他金融服务机构组成，具有oligopoly和monopolistic competition的混合市场形态。

全国性国有金融中介的所有制特点决定了其抵御风险能力优于其他金融中介，加之其市场占有率高，既有吸引存款的优势，也在信贷市场上具有一定的定价地位。因此，全国性国有金融中介可以选择风险低、回报稳定的融资服务对象，如为国有企业，区域性公共管理和其他国有机构，混合所有制金融中介等。

其他金融中介或因不具备吸引存款的优势，或因不具备吸引存款的资质，需要通过同业拆借从全国性或地方性国有银行获得流动性。其可选择的融资服务对象也有别于国有金融中介，风险相对高，坏账可能性相对大，对其要求的风险回报也高。

以上的描述隐含着在金融市场上存在分割现象（market segmentation）。金融市场分割导致了金融中介之间出现因服务对象及其融资风险而异的分工：

图6 金融部门不同所有制信贷分配机制

金融体系内的融资功能重叠和信贷关系嵌套导致该行业金融服务链长，重叠和嵌套环节中存在“过度”就业，累加的劳动力成本高，从存款到投资的功效转换过程复杂、交易成本（transaction cost）高。

金融中介的交易成本一方面会压低存款利率 r_{s} ，另一方面抬高融资便利的费率 r_{q} 。当然， r_{s} 和 r_{q}利率并非由金融中介单方面决定。以存款利率为例，若一个追求利润最大的金融中介出于自身利益压r_{s} ，则家庭的储蓄意愿会因此而降低。在竞争性市场上，储蓄利率受供需两方面的影响。金融中介和实体企业之间的利益通过借贷关系以及融资便利的费率 r_{q}联系在一起。若金融中介出于自身利益抬高r_{q} ，则投融资成本上升，实体企业的投资意愿下降。竞争性市场上融资侧的均衡利率同样受供需两方面的影响。

综上所述，一个经济体的财产收入空间由实物资产的边际产出和货币性资产的市场利率所决定。金融中介的费率（用于支付金融中介的雇员收入）越高，效率越低，社会平均财产收益率越低。

1.货币乘数效应

中央银行一方面可以通过基础货币 M_{0} ，另一方面可以通过法定存款准备金率 z 直接影响广义货币 M的规模。中央银行的再贴现政策影响市场利率（r_{Q}-收益率和 r_{s}-存款利率）波动的上下限，间接影响 M的规模。为了保证中央银行对影响广义货币规模的影响力，不受法定最低存款准备金率 z 约束的金融中介不应开展存贷款业务。 从中国的现实情况看，M_{0} 和 M 均呈上行趋势，两者正相关，说明存在乘数效应。

从 M:M_{0} 看，货币乘数有上行趋势；在若干年份 \Delta M: \Delta M_{0}呈水平或垂直关系，说明\Delta M 与 \Delta M_{0} 无关，相当于一个自主变量。广义货币 M 的自主变化说明商业银行有足够充裕的自备金，法定最低存款准备金率 z 对商业银行（或金融中介部门）没有真正的约束力。

比较广义货币量M 和全社会融资规模（aggregate financing - AF，对应金融便利 Q）发现，2016 年以后 AF 明显高于 M，即部分资金并未流出金融部门、被用于固定资产融投资或财产性消费，因此也不产生货币乘数效应。M 和 AF 之间的缺口意味着金融业内部存在信贷关系嵌套和金融服务功能重叠，拉大了r_{Q} 和 r_{S} 之间的差距，降低了金融服务效率。

设广义货币供应规模（名义量）为

M=M\left( M_{0},r_{Q},r_{S},z\right)

其中 r_{Q} 与 M 正相关， r_{s} 与 M 负相关， r_{Q} 和 r_{s} 中均剔除了物价水平变化因素。此外，经检验 z 对 M的影响确实不显著。

广义货币供应回归模型:

\Delta M=\alpha+ \beta_{1}\Delta M_{0}+\beta_{2}\Delta r_{Q}+\beta_{3}\Delta r_{S}+\varepsilon

回归结果显示：

模型残差序列有阶段性特点，与 2008 年以后广义货币 M 的自主变化有关；\Delta r_{Q} 对 \Delta M 的影响为正，\Delta r_{s} 对 \Delta M的影响为负，但均不显著；模型拟合度偏低。

根据模型的阶段性特点对回归模型，做如下修正：

\Delta M=\alpha+ \beta_{1}\Delta M_{0}+\beta_{2}\Delta r_{Q}+\beta_{3}\Delta r_{S}+\beta_{4}D_{97-08}+\beta_{5}\Delta M_{0}*D_{97-08}+\varepsilon

\begin{align*} \begin{split} D_{97-08}= \left \{ \begin{array}{ll} 1, & 1997-2008\\ 0, & otherwise \end{array} \right. \end{split} \end{align*}

修正后模型的回归结果显示：

\Delta M_{0} 对 \Delta M_{} 有影响，在 5%的水平上显著；\Delta M_{}确有两阶段特点，与 2008 年前后 TFP 的两阶段变化特点相对应；由于哑变量 D 代理了 TFP 以及实物资产边际产出的阶段性变化特点，因此\Delta r_{Q} （ r_{Q}= 实物资产边际产出 – 资产平均收益率）对\Delta M_{} 的影响不显著；\Delta r_{s} 对 \Delta M_{}的影响不显著，意味着成本因素对商业银行放贷行为没有规律性影响；2015 年和 2016 年 ΔM 的表现明显区别于其他年份。

作分阶段修正：

\Delta M=\alpha+\beta_{1}\Delta M_{0}+\beta_{2}D_{97-08}+\beta_{3}D_{09-14}*\Delta M_{0}+\beta_{4}D_{15-20}\Delta M_{0}+\mu

\begin{align*} \begin{split} D_{97-08}= \left \{ \begin{array}{ll} 1, & 1997-2008\\ 0, & otherwise \end{array} \right. \end{split} \end{align*} ;\begin{align*} \begin{split} D_{09-14}= \left \{ \begin{array}{ll} 1, & 2009-2014\\ 0, & otherwise \end{array} \right. \end{split} \end{align*}; \begin{align*} \begin{split} D_{15-20}= \left \{ \begin{array}{ll} 1, & 2015-2020\\ 0, & otherwise \end{array} \right. \end{split} \end{align*}

除 DW 值以外，回归结果令人满意:

1997 年至 2008 年，\Delta M_{0} 对 \Delta M_{} 有显著正影响（18.222→货币乘数效应）；2009 年至 2014 年（实施 4 万亿投资计划，期间政府曾力推“中国制造 2025”），\Delta M_{0} 对 \Delta M_{} 有显著负影响（18.222-19.163=-0.9403），说明商业银行在该阶段与 M_{0} “脱钩”，或存在某种体现在常数项中的“固化”因素（ t \approx16 ），自 2009 年起对 ΔM 产生影响；2015 年至 2019 年， 对 \Delta M_{}有显著“弱”正影响（18.222-11.705=6.5175），再次说明存在某种与央行货币政策并行、影响商业银行行为的“固化”因素。 哑变量D_{97-08} 代理商业银行的金融服务费率（贷款利率） r_{Q}；1997 年至 2008 年， D_{97-08}基本抵消了 常数项的影响（12959-13493=-543），\Delta M_{0} 基本“框定”了 \Delta M ，该阶段上述“固化”因素对广义货币的影响尚未体现；2008 年起，哑变量 D_{09-14} 和 D_{15-20} 相继奏效，抵消了 \Delta M_{0} 对 \Delta M_{}的影响，而常数中隐含的“固化”因素在很大程度上影响了商业银行的行为。资产平均收益率（近似视为商业银行获得资金的平均成本）变化对 \Delta M_{}没有显著影响，说明成本因素对商业银行的行为没有规律性的影响。究其原因，或是商业银行的贷款（金融服务）收益足够丰厚，或是存在某种“强制性”外部因素，导致商业银行在放贷时“不计成本”。中国的金融市场形态具有寡头（oligopoly）与垄断竞争（monopolistic competition）混合的特点，大型商业银行获取丰厚盈余是一种事实；除此之外，中央层面财经工作领导小组对信贷规模的决策可能直接影响商业银行的放贷行为。

6.政府调控经济

使用每年新增政府支出的变化情况，来衡量政府对经济运行过程中的调节力度。

图7 1997-2020年间 政府调节经济力度

从图7可以看到，政府对经济运行过程中的调节力度发生了显著的变化，大概分为三个阶段，1997-2007；2008-2012；2013-2020；不断递增的过程。

1. 财政政策- 目标与手段

财政政策（fiscal policy）主要服务于经济增长和就业，一般具有逆周期功能。下图中，分别将 GDP 增长数据与

- 按国民经济核算口径统计的国家消费 G 数据以及- 按财政口径统计的财政支出 Expenditure 数据做了对比

总体而言，同期财政支出增长率与 GDP 增长率成正比，逆周期特点不明显。此外，财政政策与货币政策之间似可更好协调（→IS-LM 模型）。

随着经济规模扩张，公共管理的任务领域也随之扩大，体现在政府财政支出上。此外，财政政策还具有逆周期功能 ― 当经济疲软时，政府应扩大财政支出、拉动需求；vice versa。随公共管理任务领域扩大而扩大的财政支出具有长期性、秩序性特点；与逆周期有关的财政支出具有短期、过程性特点。

设国家消费在 GDP 中的占比为μ ，体现秩序性政策特点，

回归模型 1：国家消费 G 与 GDP 的关系

G=\alpha+\beta GDP+\varepsilon

截距项不等于 0；残差项显示，G 以 2010 年为界具有两阶段特点。

G=\alpha+\beta_1 GDP+\beta_2 D_{97-10}+\beta_3 GDP*D_{97-10}+\varepsilon

\begin{align*} \begin{split} D_{97-10}= \left \{ \begin{array}{ll} 1, & 1997-2010\\ 0, & otherwise \end{array} \right. \end{split} \end{align*}

残差序列正相关，或与上世纪末财政政策被用于支持体制转换过程有关。

模型各项检验指标均好，能够再现过去二十多年财政支出的特点：

-第一阶段，1996 至 1998 年G 在 GDP 中的占比平均约为 14.0%；1998 年 G 上行有逆周期（亚洲金融危机）特点；-第二阶段，1999 年至 2010 年G 在 GDP 中的占比上升为平均约 15.3%，或与支持国企改制以及公共任务领域随经济规模扩张而拓展有关；但段内 G:GDP 呈持续下降趋势，可以视作政府对经济过程干预减少的“市场化”表现；-第三阶段，2011 年至 2019 年G 在 GDP 中的占比上升为平均约 16.1%，且段内 G:GDP 呈持续上升趋势；对此，一种解释是公共任务领域随经济规模扩张而进一步拓展；另一种解释是政策干预渐趋频繁，与第二阶段相反，有“逆市场化”表现。

上述三个台阶的 G:GDP具有秩序性政策调整的特点，用F_O （order）代理；各阶段内G:GDP 的波动具有过程性特点，用 F_P （process）代理，G 由 F_O 和 F_P 构成。

\hat F_O= \frac{\hat G-\alpha}{\hat \beta}

从残差项中分离出 \hat F_P= \hat F_P\left( \hat \varepsilon \right)（取值 -1 对应紧缩，0 对应中性，+1 对应扩张）。

G 的秩序性和过程性特点:

G=\hat F_O+\beta \hat F_P+\epsilon

- G 在 GDP 中占比（三阶段）跳跃式提高，体现了 lags 效应（a la Timm）；

- 第一至第二阶段的跳跃与上世纪末至本世纪初国企改制中的财政补贴不无关系；

- 2010 年以后 G 在 GDP 中的占比再次提高，原因应为财政政策的秩序性调整。

从 F_O在 GDP 中的占比看，在 1996 年至 1998 年以及 1999 年至 2010 年两个阶段内有上升趋势，2010 年以后基本停留在同一个水平上。

从 F_P在 GDP 中的占比看，除了 1998 年（亚洲金融危机）和 1999 年至 2002 年（国企改制），在其他年份基本少有明显扩张或紧缩的表现。

- 秩序性因素决定的三台阶财政支出 FO和（左图，Wagner）

- 伴随经济规模扩张连续（滞后）变化的公共支出效应（右图，Timm）。

2. 政策效果的讨论

1） 上期 GDP 实际增长率与当期 G 名义增长率总体正相关，仅在少数年份负相关（逆周期），因此可以判断 G 不具明显的逆周期特点；

2） 同期 GDP 名义增长率与 G 名义增长率总体正相关，与国民经济核算方法以及政府财政预算有关；

3） 下期 GDP 名义增长率与当期 G 名义增长率无可识别的相关性，说明 G 没有明显的逆周期效果，与 1）的判断相符。

G 中隐含秩序性政策意图，而秩序性政策的功能显然不是逆周期，而是影响中长期经济运行。

从上图中发现，FO的第二阶段对应中国经济高增长周期，第三阶段对应经济增长率疲软周期。对比 FO和 TFP，得到的结果类似。

3. 货币政策

货币政策（monetary policy）和财政政策一起，构成了宏观经济政策的两大支柱。货币政策的主要目标一是稳定物价，二是助力经济增长。中国货币政策的制定和实施者是中央银行 ― 中国人民银行，下属于国务院。这里需要额外说明，大部分发达国家的央行独立于政府，目的是保证央行的独立性，避免货币政策成为附属于财政政策的工具。 货币政策主要包括以下手段：

- 再贴现政策，主要功能是框定货币市场利率 r 的波动幅度，

- 公开市场业务，主要功能是影响货币基础 M0，

- 最低存款准备金率，主要功能是影响广义货币 M。

物价水平 P 与 M0以及 M 之间存在正向关，但 ΔP 和 ΔM0之间似无可识别的相关性。 ΔP 和 ΔM 之间 2008 年以前基本正相关；之后基本负相关，似乎不是纯货币现象，而与实体经济运行状况有关。 从以上推测：中国人民银行货币政策的目标取向首先是稳定实体经济运行，其次是稳定物价水平。

回归模型 1：国家消费M_0 与 GDP 的关系

M_0=\alpha+\beta GDP+\varepsilon

从残差序列正相关、且有两阶段特点看，货币政策可能被用于干预经济过程。

- 1996 年至 1999 年 v 下行，2000 年和 2001 年 v 略微回升，2002 年和 2003 年 v 又再次下行；该阶段 v 波动的原因不应是公众持币习惯反复变化，而是在

✓ 重构社保体系，

✓ 亚洲金融危机，

✓ 国企改制等

2003 年以后， v_0 除了在 2009 年出现下降外，整体呈上升态势；该阶段 v_0 变化的主要原因应是支付手段发生了持续改变。

截距项不等于 0；残差项显示，G 以 2010 年为界具有两阶段特点。

\nu_0=\alpha+\beta_1 GDP+\beta_2 D_{97-03}+\beta_3 GDP*D_{97-03}+\varepsilon

\begin{align*} \begin{split} D_{97-03}= \left \{ \begin{array}{ll} 1, & 1997-2003\\ 0, & otherwise \end{array} \right. \end{split} \end{align*}

与实际 v0之间的偏差体现货币政策的过程性干预

从以上分析中得出结论：

1） 中国货币基础 M0的周转率总体呈上升趋势；

2） 近 20 年以来，货币政策的表现总体符合国务院的“稳健”要求；以下年份央行曾动用货币政策干预经济过程：

- 2008 年前后，货币政策紧缩与当时经济过热有关；

- 2012 年和 2013 年，货币政策扩张与 4 万亿投资刺激经济以后增长率下滑有关；

- 2016 年，货币政策扩张的原因与 2012 年和 2013 年类似（曾用房地产拉需求，诱发房价快速上涨，负债率过度提高，但对国民经济未产生积极作用）；

- 2018 年，货币紧缩政策与降负债率（“去杠杆”）有关。

4.货币政策效果

货币政策首先影响广义货币 M 和市场利率 r ，然后通过市场利率 r影响需求（尤其是投资需求），最后通过需求拉动供应（收入或 GDP）。虽然货币学派（芝加哥学派，代表人物 Friedman）认为货币也是生产要素，M 会直接影响供应；但经济学主流并不认同这一观点。以下按照新古典主义综合的思路（IS-LM 模型）分析货币政策的效果。

回归模型 1：流动性需求

\Delta L=\alpha+\beta_1 \Delta GDP+\beta_2 \Delta r_s+\mu

其中， \Delta L=M2_{t}^{}-M2_{t-1}^{} ,表示的是货币的流动性需求。

回归结果显示：\alpha 不显著；残差序列弱正相关，且残差项方差在 2009 年和2015 年出现两次变化（异方差），与之前研究的阶段性特点吻合。

将模型分为三阶段后，利率 r_s变化对流动性 L 变化的影响不显著。因此略去\Delta r_s ：

基于以上考虑，对回归模型进行修正，实际修正模型如下所示：

\Delta L=\alpha+\beta_1 \Delta GDP+\beta_2 D_{97-08}+\beta_{3} D_{09-14} \Delta GDP+\beta_4 D_{15-20} \Delta GDP+\mu

\begin{align*} \begin{split} D_{97-08}= \left \{ \begin{array}{ll} 1, & 1997-2008\\ 0, & otherwise \end{array} \right. \end{split} \end{align*} ;\begin{align*} \begin{split} D_{09-14}= \left \{ \begin{array}{ll} 1, & 2009-2014\\ 0, & otherwise \end{array} \right. \end{split} \end{align*}; \begin{align*} \begin{split} D_{15-20}= \left \{ \begin{array}{ll} 1, & 2015-2020\\ 0, & otherwise \end{array} \right. \end{split} \end{align*}

回归结果如下所示：

\Delta r_s （资产平均回报 → 谨慎动机和投机动机）对 ΔL 无显著影响；1997 年至 2008 年， ΔL 主要取决于交易动机（ ΔGDP ），与 ΔGDP无关的流动性变化甚微；2009 年至 2014 年，ΔGDP 对 ΔL 的影响为负，显然不符合经济逻辑；2015 年至 2019 年亦然；与此同时，与 ΔGDP 无关的 \alpha 达到 16080，大于 ΔL ，说明 ΔL 与 ΔGDP 脱钩；

对比 ΔGDP 和 ΔL 可以发现（见下图），某些年份 ΔGDP 回落、ΔL 上升；另一些年份ΔGDP 上升、ΔL 回落，两者均与交易动机无关；ΔL 的“异常”变化显然不能解释为随机波动，否则残差序列不应负相关（DW=2.35）。

基于以上讨论，分析式的残差波动，并增加一个可能与广义货币供应有关、交替取值-1 和 1 的变量 cycle：

基于以上考虑，对回归模型进行修正，实际修正模型如下所示：

\Delta L=\alpha+\beta_1 \Delta GDP+\beta_2 D_{97-08}+\beta_{3} D_{09-14} \Delta GDP+\beta_4 D_{15-20} \Delta GDP+\beta_5 cycle+\mu

\begin{align*} \begin{split} D_{97-08}= \left \{ \begin{array}{ll} 1, & 1997-2008\\ 0, & otherwise \end{array} \right. \end{split} \end{align*} ;\begin{align*} \begin{split} D_{09-14}= \left \{ \begin{array}{ll} 1, & 2009-2014\\ 0, & otherwise \end{array} \right. \end{split} \end{align*}; \begin{align*} \begin{split} D_{15-20}= \left \{ \begin{array}{ll} 1, & 2015-2020\\ 0, & otherwise \end{array} \right. \end{split} \end{align*}

回归结果如下所示：

式的回归结果证实了 2008 年以后的 ΔL 不能用交易动机解释。因此判断，广义货币增量自 2009 年起并非由货币市场的供需协调所决定，而主要取决于（广义）货币供应方的行为。

为了找出引起 ΔL 波动（cycle）的原因，再次回到广义货币的供应行为。式的残差序列负相关（DW=2.27）说明，对 ΔM 存在交替变化的外生变量。由于商业银行信贷规模直接影响广义货币量，因此上述外生变量是除了货币基础M0和存贷款利率（对ΔM无显著影响）以外、另一个可以直接干预信贷规模的变量 ― 信贷政策变量（非常规政策变量）记作 CP。根据似然原则对 CP取值如下 :

基于以上考虑，对回归模型进行修正，实际修正模型如下所示：

\Delta L=\alpha+\beta_1 \Delta M+\beta_2 D_{97-08}+\beta_{3} D_{09-14} \Delta M+\beta_4 D_{15-20} \Delta M+\beta_5 C_p+\mu

\begin{align*} \begin{split} D_{97-08}= \left \{ \begin{array}{ll} 1, & 1997-2008\\ 0, & otherwise \end{array} \right. \end{split} \end{align*} ;\begin{align*} \begin{split} D_{09-14}= \left \{ \begin{array}{ll} 1, & 2009-2014\\ 0, & otherwise \end{array} \right. \end{split} \end{align*}; \begin{align*} \begin{split} D_{15-20}= \left \{ \begin{array}{ll} 1, & 2015-2020\\ 0, & otherwise \end{array} \right. \end{split} \end{align*}

回归结果如下所示：

回归结果显示， C_p 通过影响信贷规模对 ΔM 产生（显著）影响；后者进一步对 ΔL ― 在式中体现为中介变量 cycle ― 产生影响。

比较 C_p和L \Delta L 的取值可知， C_p 对 ΔL 的影响在 2010 年以后表现趋弱，反映了同期银行同业拆借规模扩大（银行系统内的借贷关系不影响广义货币量）。

在之前对广义货币供需两方面的分析中均发现，在 2008 年以后存在某种“固化“因素，抵消了ΔM_0 对 ΔM 以及 ΔGDP 对 ΔL 的影响。

如上图所示，除少数年份外 μ 整体呈上升趋势，可以理解为商业银行释放其贷款能力，使得货币乘数效应相应放大。同期，广义货币的周转率从接近 1 降至 0.5，意味着广义货币中的一半并未在商业银行和公众之间周转，而是静止于金融体系内部或是在商业银行之间周转，形成了一种“货币陷阱”。

由于广义货币乘数有加速趋势（或广义货币周转率有减速趋势），且金融体系内存在不受货币政策影响的“货币陷阱”，因此 M 的变化与 GDP 的变化渐行渐远，在 2008 年以后几乎与实体经济运行脱节。这就是影响广义货币增量的“固化”因素所在，而“固化”因素的原因在金融体系内部。用信贷政策直接干预商业银行行为和信贷规模或是是政府别无选择的结果。

至此可以得到结论：由于金融系统内部存在”广义货币陷阱”，利率对此没有显著影响，因此货币政策失灵。

7. AD-AS模型

7.1 Keynesian Theory ― Multiplier Effect 模型

采用 1978 年至 2019 年数据的回归结果。其中：intercept 不显著；拟合度为 99.66%，残差序列正相关。intercept 不显著的原因可能是数据样本的时间跨度过长，C_0发生了变化；残差序列正相关的原因可能是模型中缺少了不应忽略的解释变量。将数据样本数减少到 1997 年至 2019 年，回归结果也是如此表现，显然，缩短样本长度未能解决问题。因此采用准动态分析方法，用增量替代总量描述消费行为。

私人消费增量模型 ：

\Delta c=\alpha +\beta_1\Delta y+\varepsilon

增量模型的 intercept 不显著，消费倾向 β 显著，拟合度近 92%，残差序列正相关。 通过第二章（B）的分析已知，私人消费除了与收入有关外，和收入分配有关；第三章（C）分析了全要素生产率，其变化影响产出、进而影响要素收入。此外，通过第二章（B）的分析还发现，2014 年至 2016 年私人消费因财产性消费“异常”上扬（见上图，ΔGDP 和 ΔGDP-ΔC 曲线），与当时经济增长率下滑、用房地产拉动内需有关。

基于以上考虑，对回归模型进行修正，实际修正模型如下所示：

\Delta C=\alpha+\beta_1 D_{97-10} \Delta Y+\beta_2 D_{11-13} \Delta Y+\beta_3 D_{14-16} \Delta Y+\beta_4 D_{17-20} \Delta Y+\mu

\begin{align*} \begin{split} D_{97-10}= \left \{ \begin{array}{ll} 1, & 1997-2010\\ 0, & otherwise \end{array} \right. \end{split} \end{align*} ;\begin{align*} \begin{split} D_{11-13}= \left \{ \begin{array}{ll} 1, & 2011-2013\\ 0, & otherwise \end{array} \right. \end{split} \end{align*}; \begin{align*} \begin{split} D_{14-16}= \left \{ \begin{array}{ll} 1, & 2014-2016\\ 0, & otherwise \end{array} \right. \end{split} \end{align*} \begin{align*} \begin{split} D_{17-20}= \left \{ \begin{array}{ll} 1, & 2017-2020\\ 0, & otherwise \end{array} \right. \end{split} \end{align*}

在 1997 年至 2020年，中国的私人消费倾向有如下变化：

- 1997 年至 2010 年的平均消费倾向为 0.2829，该阶段资产收入份额上升；- 2011 年至 2013 年的平均消费倾向为 0.3649，该阶段劳动收入份额上升；- 2014 年至 2016 年的平均消费倾向为 0.4916，该阶段 Pigou 效应十分明显；- 2014 年至 2019 年的平均消费倾向为 0.3797，可理解为“新常态”。中国分阶段平均消费倾向

利用上式的估计结果，根据支出法建立乘数效应模型：

\Delta Y= \Delta C+\Delta G+\Delta I+\Delta NX

\Rightarrow\Delta Y= \Delta \hat C_0+\beta_1 D_{97-10} \Delta Y+\beta_2 D_{11-13} \Delta Y+\beta_3 D_{14-16} \Delta Y+\beta_4 D_{17-20} \Delta Y+\Delta G+\Delta I+\Delta NX

\Rightarrow\Delta Y=\frac{1}{1-\sum_{i=1}^{4}{\hat \beta_iD_i}} (\Delta \hat C_0+\Delta G+\Delta I+\Delta NX )

\Delta \hat C_0 做数值校准, 回归方程如下：

\Delta Y=\sum_{i=1}^{4}{\gamma_i*D_i} (\Delta \hat C_0+\Delta G+\Delta I+\Delta NX )+\mu

\begin{align*} \begin{split} D_{97-10}= \left \{ \begin{array}{ll} 1, & 1997-2010\\ 0, & otherwise \end{array} \right. \end{split} \end{align*} ;\begin{align*} \begin{split} D_{11-13}= \left \{ \begin{array}{ll} 1, & 2011-2013\\ 0, & otherwise \end{array} \right. \end{split} \end{align*}; \begin{align*} \begin{split} D_{14-16}= \left \{ \begin{array}{ll} 1, & 2014-2016\\ 0, & otherwise \end{array} \right. \end{split} \end{align*} \begin{align*} \begin{split} D_{17-20}= \left \{ \begin{array}{ll} 1, & 2017-2020\\ 0, & otherwise \end{array} \right. \end{split} \end{align*}

中国乘数效应

- 需求导向的乘数效应模型可以再现中国经济运行特点，说明确实存在供应能力过剩；

✓ 1997 年至 2010 年的实际乘数为 1.386，按消费倾向 \hat c折算的理论值为 1.394，前者较后者低 0.6%，

✓ 2011 年至 2013 年的实际乘数为 1.570，按消费倾向 \hat c 折算的理论值为 1.574，前者较后者低 0.3%，

✓ 2014 年至 2016 年的实际乘数为 1.953，按消费倾向\hat c 折算的理论值为 1.967，前者较后者低 0.7%，

✓ 2017 年至 2019 年的实际乘数为 1.608，按消费倾向 \hat c折算的理论值为 1.612，前者较后者低 0.2%；

- 2014 年至 2016 年消费倾向上升及其乘数效应变大的原因是财产性消费；

放任房地产投机，以期拉动需求的做法不可取、不能持续，不仅因为财产性消费会 引起对其他消费需求的替代（预算约束）和对生产性投资的挤压（融投资成本上升），也会对收入、尤其对资产存量产生与公平原则相悖的实际再分配效果（实物资产涨价相当于货币资产贬值，持实物资产者得益，持货币资产者受损）。

- 近年来，需求拉动供应的乘数约为 1.6，产能过剩问题仍然存在。

7.2 Neoclassical Synthesis ― AD-AS 模型

从微观基础（Microeconomic Foundation）看，金融市场发育不健全，利率未能有效调节资金供需，因此 IS-LM 模型与中国现实不符。以下重点介绍和验证 AD-AS 模型。

对净出口 NX 未做基础分析，一方面是因为影响 NX的因素颇多，外部因素如美国次贷、金融危机和因此而起的全球经济危机、欧洲主权债务危机等，内部因素如汇率松动、市场化逆转、政策干预再度加强等；另一方面是因为NX占 GDP 份额较小（2007 年曾达到近 8.7%，近年约为 2%上下），在分析 AD-AS 关系时影响不显著。因此将NX 设为“自主” 变量（autonomous variable）。

回归模型 1：事后均衡的价格水平变化模型

\Delta P_t=\alpha+\beta_1 P_{t-1}+\beta_2 \Delta F_{O_t}+\mu_t

回归结果显示：

- 价格预期（前期价格水平 P_{t-1} ）与价格水平变化 ΔP_t负相关，原因是可预料的价格变化会使财产性消费和投资提前，影响后继供需行为和供需对比关系；

- 带有秩序性政策特点的财政支出 F_O 与 ΔP 正相关，原因是 ceteris paribus（c.p.）国家消费的挤出效应（crowding out effect）。

由于回归式拟合度偏低，且前半期残差序列有上行趋势，因此修正如下：

\Delta P_t=\alpha+\beta_1 P_{t-1}+\beta_2 \Delta F_{O_t}+\beta_3 \Delta F_{O_t}* D_{00-10}+\mu_t

\begin{align*} \begin{split} D_{00-10}= \left \{ \begin{array}{ll} 1, & 2000-2010\\ 0, & otherwise \end{array} \right. \end{split} \end{align*}

验证结果显示，体现在 \Delta F_{O_t}回归系数上的挤出效应在 2000 年至 2010 年期间为 0.0164， 2011 年至 2019 年较低，为 0.0119，原因是后半期的供应过剩问题较前半期明显。

由于 1999 年和 2009 年的价格波动与外部冲击不无关系（亚州金融、经济危机和美国金融、经济危机），因此将其单独列为 impacts：

\Delta P_t=\alpha+\beta_1 P_{t-1}+\beta_2 \Delta F_{O_t}+\beta_3 \Delta F_{O_t}* D_{00-10}+\beta_4 *impacts+\mu_t

回归模型 2：事后均衡的收入（GDPGNP）水平变化模型

\Delta Y_t=\alpha+\beta_1 P_{t-1}+\beta_2 \Delta F_{O_t}+\mu_t

上式残差项标准差在2011年出现一个跳跃，或与之前讨论的FO挤出效应有关，因此修正如下：

\Delta Y_t=\alpha+\beta_1 P_{t-1}+\beta_2 \Delta F_{O_t}+\beta_3 \Delta F_{O_t}* D_{11-18}+\mu_t

\begin{align*} \begin{split} D_{11-18}= \left \{ \begin{array}{ll} 1, & 2011-2018\\ 0, & otherwise \end{array} \right. \end{split} \end{align*}

修正后， ΔF_O在 2011 年以前的回归系数为 5.3324，2011 年至 2018 年为 4.5602，说明国家消费拉动供应的效果变弱。 观察回归结果还发现，2000 年至 2007 年残差序列有上行趋势，或与同期 TFP 上行、供应的价格敏感度有关。根据这一推测，再次修正式:

\Delta Y_t=\alpha+\beta_1 P_{t-1}+\beta_2 \Delta F_{O_t}+\beta_3 \Delta F_{O_t}* D_{11-18}+\beta_4D_{00-07}*P_{t-1}+\mu_t

\begin{align*} \begin{split} D_{11-18}= \left \{ \begin{array}{ll} 1, & 2011-2018\\ 0, & otherwise \end{array} \right. \end{split} \end{align*} \begin{align*} \begin{split} D_{00-07}= \left \{ \begin{array}{ll} 1, & 2000-2007\\ 0, & otherwise \end{array} \right. \end{split} \end{align*}

- 与 Pt-1有关的 ΔY 份额 ― 可理解为市场调节的结果 ― 有下行趋势，

- 与 F0有关的 ΔY 份额 ― 可理解为政策干预的结果 ― 有上行趋势

另一个值得注意的现象是，在式中 intercept 显著为负。政策干预作用趋强和市场调节作用趋弱是 ΔY 具有 inherent 下行趋势的原因。

由于政策干预能够拉动需求、释放过剩产能，短期见效，因此政策制定者有“干预偏好”。但是政策干预会弱化市场功能，“架空”市场又导致微观层面的经济活力进一步趋弱、政策干预的作用被进一步放大，使经济过程进入“螺旋向下”循环。如果没有更全面、彻底的秩序性政策改革，则经济过程本身难以从“螺旋向下”的循环中自拔。 从以上回归结果可以看出，中国经济的短期走向取决于上期状态和当期政策干预力度，设置 ΔF_O 的 scenarios 即可推算相应的 ΔP 和 ΔY，但不能预测经济增长趋势。

8.中国经济现状

经过对中国经济微观基础、宏观总量和增长分析可以做出如下判断：

1） 分析期内中国经济保持了较高的增长速度，但未来走向并不乐观，

2） 货币政策失灵，财政政策过度干预导致出现市场被“架空”迹象，

3） 就业中存在赘余，干扰要素配置，

4） 实物资产存量中存在低效产能，或实物资产利用效率偏低，

5） 金融（商业银行）体系内存在流动性陷阱，货币资产向实物资产的转换效率偏低，

6） 家庭部门储蓄率偏高，原因在于未来不确定偏大，狭义的再分配政策和广义的社会政策尚需进一步完善，

解决上述问题，不能仅仅依靠过程政策，设计、重构经济秩序更为重要。中国经济需要更深入、更全面的改革。