一、引论

1、属性数据

属性变量具有由类的集合组成的度量量表，如在满意度调查中的满意、一般、不满意；在性别数据中的男、女。这类数据在我们日常生活中非常的常见，其数据领域涵盖了各行各类。但是对这些数据也有一定的划分，分别为有序量表和名义量表。

有序量表：指数据具有自然的顺序，如治疗效果（很好、好、一般）；名义量表：非有序量表的数据称为名义量表，如上下班方式（自驾、公交、地铁）；性别（男、女）

2、优势比

对于各属性的好坏我们有其度量的方式——优势比

（1）定义

对于成功的概率 π\pi ，成功的优势定义为

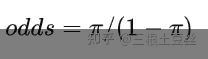
则其优势比定义为

（2）性质

设第一类事件成功的概率为 π1\pi_1 第二类事件成功的概率为 π2\pi_2得到其优势比θ\theta ，若 1">θ>1\theta>1 则说明第一类事件比第二类事件更容易成功，反之也成立。且若 θ=0.25\theta=0.25，则可以认为第一类事件成功的优势是第二类事件成功的都是的0.25倍，也就是说第二类事件成功的优势的第一类事件成功优势的4倍。

3、logistic模型

设事件成功的概率为 π(x)\pi(x) ,表示不同的 xx 值处成功的概率，则logistics回归模型的线性表示有

则 π(x)\pi(x) 的公式则表示为

例如：得到模型拟合结果为

则有

其 0">β>0\beta>0 可知其优势会随着x值的增大而增大，要求出某x值的优势可以将其具体值带入计算，这类不做过多计算。

在这里贴上各模型更加详细的原理介绍

三根土豆丝：属性数据分析理论基础3 赞同 · 1 评论文章

二、实际操作

1、名义响应变量模型

对于名响应变量的模型我们只需要找到各响应变量之间的优势比，则可以知道哪个变量对模型的影响更加显著。首先我们先来分析数据，我们使用到的数据是泰坦尼克号的乘客数据（ps:这里的数据可能不是很好，拟合的模型不具备统计参考价值），在这里我们只截取了一小部分的分类变量进行拟合模型。

在这里其数据的类别应为三类，但是这里我们只截取了两类数据，所以这个数据可以用来做二元logistic模型，如果为多类数据则需要使用多元logistic模型，这里我们需要注意，如果不注意这里会报错。显然在数据的变量中存在着两种类型的数据，一类的名义响应变量的数据也叫分类数据，一类是年龄这种连续型的数据，而且分类数据也还没有设置哑变量，所以我们要对其进行处理。在有些SPSS的版本在转换窗口可以自行的设置虚拟变量（顺带一提）。

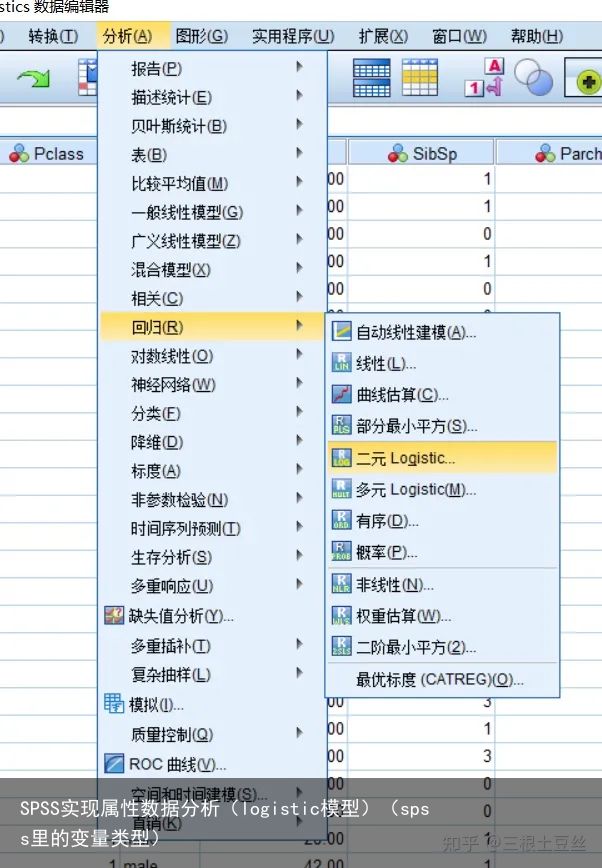
通过点击分析->回归->二元logistic回归调出模型拟合的窗口。

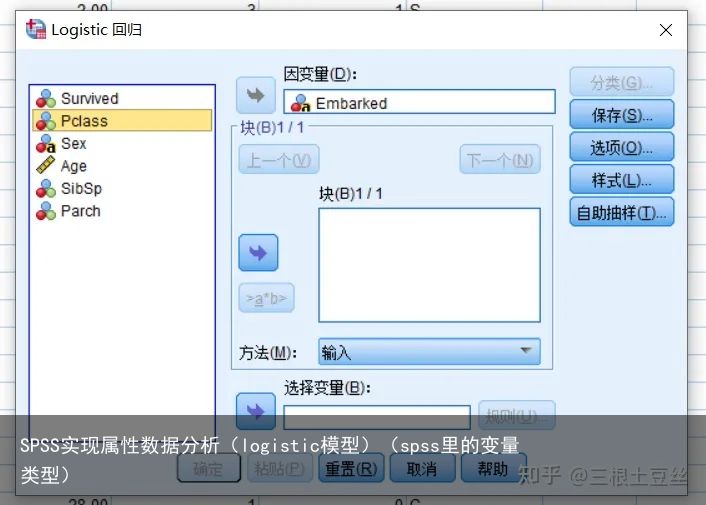
放入自变量后选择分类窗口，我们需要在这个窗口完成哑变量的设置。将分类变量放入，年龄属于连续变量，所以这里就不放入。

值得注意的是我们这里还可以选择基线的类别，而选择的这个基线的类别就是我们后期比较的时候所要比较的对象。

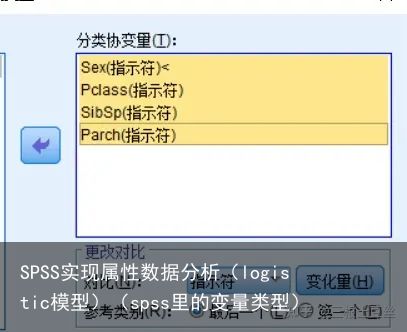
这些做完之后可以在保存窗口存下一些有用的数据，这里就不过多赘述。主要要将的是在选项窗口中我们需要选择霍斯莫-莱梅肖拟合优度，这个可以对模型的拟合优度进行检验，来判断模型的拟合效果。

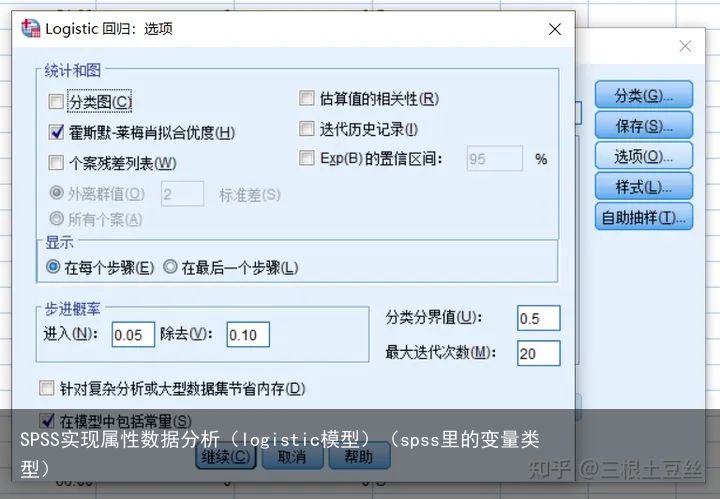
做完上面这些后，下面看模型结果。

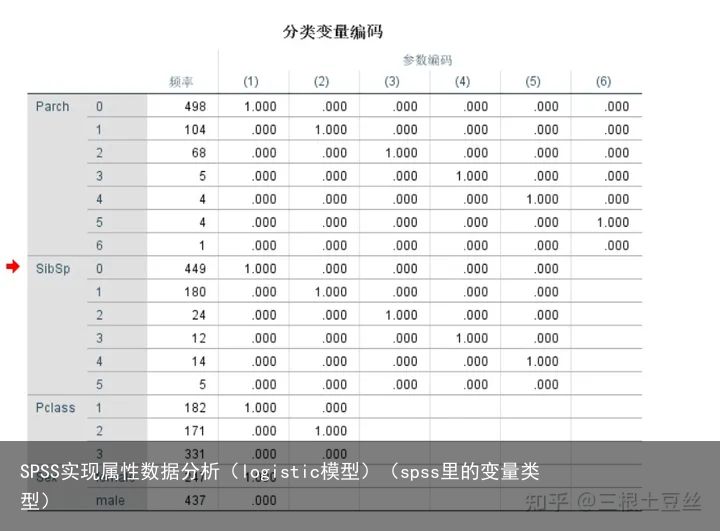
首先较为重要的是分类的变量编码，这里要注意我们在分类之前所选择的是按照最后一类进行分类，所以这里得到的结果如性别，则是按照女性表示为0，男性表示为1。

我们可以找到这样一个因子变量编码表，或者内部因子变量编码，这连个表的区别不大。这里要注意的是我们要清楚这里“C”这一类被编码为0，“S”这一类被编码为1。这里要注意，在后续的比较中我们是要时刻参考这个的，如"C"表示死亡，"S"表示存活的话，那么就有某一类能存活下来的优势是另一类（基线）存活下来优势的多少倍。

在上面的图中我们可以看到模型的拟合情况，是模型的卡方检验图，这个卡方检验的原假设是模型的拟合状况良好，被择假设是模型的拟合状况不好。在这里模型的显著性大于0.05，所以在95%的显著性水平下接受原假设认为模型的拟合状况良好，若模型的显著性小于0.05则模型不具备参考价值。

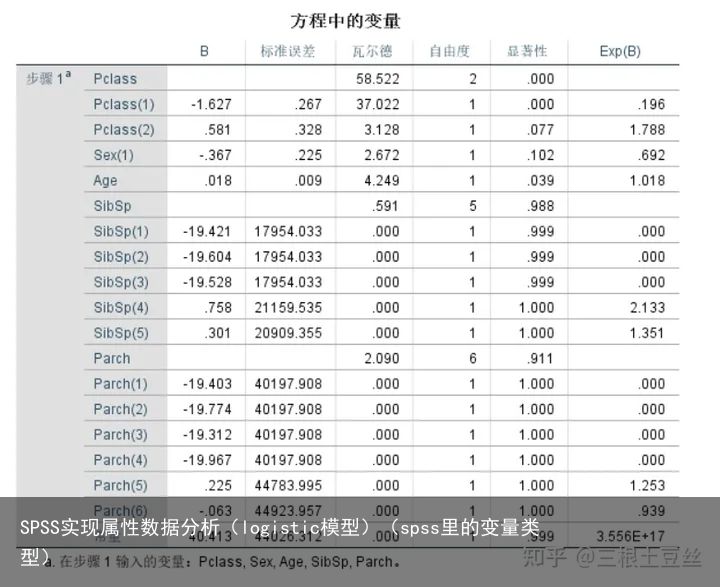
最后我们看到模型的变量系数图，在本次模型拟合中使用的数据不是很好，所以得到的结果也一般。但是这里不影响我们的解读。我们在表中的显著性检验中发现只有Pclass（1）这一类通过了显著性检验。而其系数“B”则是该类与Pclass（3）（基线）这一类的优势比为-1.627，而最后一列Exp(B)则为其优势为0.196。在这里我们可以说Pclass为Pclass（1）的这一类人能存活下来的优势是Pclass（3）这一类存活下来优势的0.196倍。

在这里年龄的显著性水平也小于0.05，说明年龄也是其影响因素之一，在这里我们可以说每增加一个单位量的年龄（即每增长一岁）则存活下来的优势增长1.018倍。

对于其他类别显著性水平大于0.05的则是对模型拟合没有显著性影响的一类，认为怎么改变对不会增加其存活的概率。

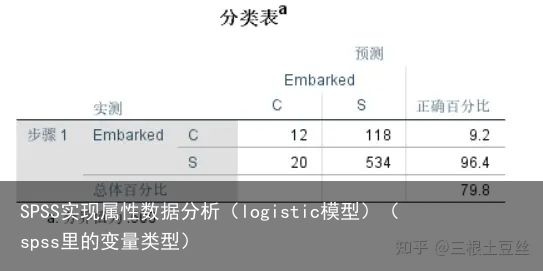
除去上面那些分析，我们还可以看到这张分类表，这是一张2×2的列联表，可以通过他计算模型的AUC值来判断模型的预测情况。

下面我们看多元logistic回归，在这里就简略的讲一下。通过点击分析->回归->多元logistic回归调出模型拟合的窗口后。在因变量有多个类别才会使用到多元logistic模型。而且我们还需要注意，对于连续型的变量我们要拟合的话我们要放入到协变量中去

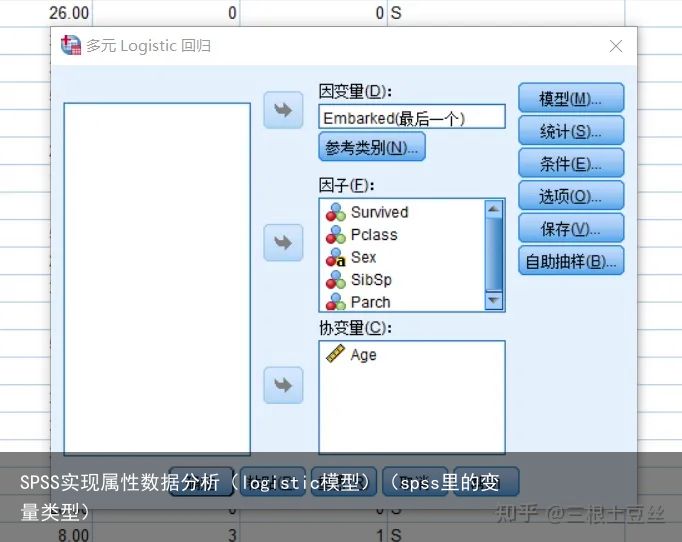
在因变量类别参考这里默认是以最后一类作为参考的类别，可以通过这个窗口手动修改。这里我们不做修改

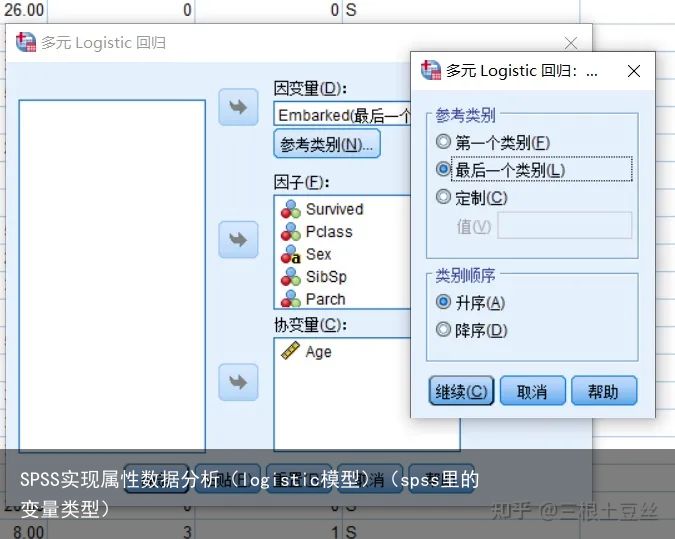
下面我们看模型结果：

通过模型的拟合可以看到模型的显著性小于0.05，值得注意的是，在这里我们的原假设是模型没有较好的拟合优度，被择假设是模型有较好的拟合优度，在这里我们要拒绝原假设认为模型有较好的拟合优度，区别于上面的二元logistic回归。

似然比检验表，这里说明的是我们所引入的变量对于模型来说是否是有效的，这里的原假设是引入的变量对模型是无效的，被择假设是对模型的影响是有效的，就是说如果似然比检验的结果大于0.05，则说明该变量对模型的影响不显著。

接下来我们看参数估计表，在这里如何判断与二元logistic几乎没有差别，例如，假设"C"为存活，“S”为死亡“Q”为失踪。则我们可以知道Pclass=1时能够存活下来而非死亡的优势是Pclass=3存活下来而非死亡优势的4.404倍。Pclass=1时失踪而非死亡的优势是Pclass=3失踪而非死亡优势的0.164倍。在这里我们还可以比较Pclass=1时存活而非失踪的优势是Pclass=3存活而非失踪优势的\frac{4.404}{0.164}=41.54 倍。

2、有序响应变量模型

有序响应数据，首先我们需要明白什么是有序响应数据，其指的是有明显的顺序的数据，如好、一般、不好。这类型的数据需要到有序响应数据的模型。在这里我们也要注意什么时候需要到有序logistic回归（累计效应模型），在因变量为有序变量时我们才会用到有序logistic模型。如果自变量为无序的，那么我们可以选择二元或多元logistic模型。

这里我们依旧拿之前的数据，虽然数据不是很好，但是不影响分析。

分析->回归->有序，调出有序logistic模型的操作窗口

在应变量这里我们应该放入有序的变量数据，而因子和协变量和前面的多元的一样，因子放入分类变量、协变量放入连续变量。

在输出的窗口，我们要勾选上我们的平行线检验，这里非常重要。

其他可以不修改，下面我们看一下模型的拟合结果：

在模型拟合信息表中我们可以看到，这里的卡方检验显著性我们可以看到其显著性小于0.05，认为其模型拟合良好，具有统计学意义。

从模型的拟合优度表中可以对模型的拟合优度做卡方检验，这里模型拟合优度卡方检验小于0.05，这里认为模型具有良好的拟合优度。

平行线检验是验证因变量之间是有序的，是logistic回归的前提条件，在这里原假设为模型符合平行性，而被择假设为模型不符合平行性，在这里我们的显著性小于0.05则拒绝原假设说明模型之间不符合平行性，所以这里的模型得到的参数估计结果就没有意义。在这里我们可以解决的方法有更换为无序模型，或剔除部分变量。在这里我们假设其显著性大于0.05，继续接下来的分析。

通过模型的检验没有问题后我们看到参数估计表，在这里所能得到的结果解读分析，如Pclass=1这一类相对于因变量结果程度的改变更大的优势是Pclass=3这一类相对于因变量结果程度的改变更大的优势的exp(-1.228)=0.292倍。

引用：

《属性数据分析引论》