一、列联表

1、优势比

优势是一组特定发生的可能性，对于成功的概率 π\pi ，成功的优势odds的定义

如π\pi=0.75,则其成功的优势为0.75/0.25=3

而优势比为一个事件发生的概率对于另一组事件发生概率的比值

样本的优势比等于各行样本优势比，则其样本的优势比的估计可以为

2、相对风险

在2×2的列联表中，相对风险就是比率

相对风险与优势比之间也有着一定的关系

二、广义线性模型

广义的线性模型中有着较多的分类，没种分类可以应对不同的数据，类似与本文重点讲解的属性类型的数据使用的logistic模型，或者之前提到过的线性模型

1、线性概率模型

线性概率模型是通过最小二乘算法拟合的回归模型，其也可以称为线性回归模型，对于二分响应变量，类型的模型为

称之为线性概率模型，因为事件发生的概率随着 x 线性的改变

线性模型的特点是简单，但是这也成为了局限其用途的地方，这个模型使用在分类变量中会有明显的结构缺陷，因为其自变量和应变量之间的关系一般是非线性的

2、logistic 回归模型

由于自变量和因变量的值通常的非线性的，而不是线性的，当x在0或1附件时，x一定量的改变产生的影响将会比x在区间中间时的影响小

这是logistic回归函数，公式使用的是指数函数，而其回归模型为

后面会重点讲解其模型的各类情况的使用方法

下面是其函数模型的概率分布曲线图

3、probit 回归模型

另一种具有类似与logistic 回归模型曲线的曲线模型，模型的联系函数称作probit联系，它将概率变换为标准正态分布z-值，方程为

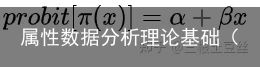
从应用的角度看，probit模型与logistic模型提供相同的拟合，其模型相似

三、简单logistic模型及模型检验

1、一元logistic回归

公式：

上面我们了解到关于logistic模型的函数函数表达式，我们拟合模型得到的参数结果为线性表达式并不是我们所需要的结果，我们需要将其还原为，概率的形式如下

其中 β\beta 表示x每增加1厘米，logit就增加 β\beta ，大多数情况不使用这结论，应为其优势的直线变化对我们来说没有太大的用处，且其优势变化是不自然的，参数 β\beta 决定s型曲线 π(x)\pi(x) 的上升或下降的速率，其符号正负表示为上升或者下降

模型特殊点：

当 β\beta =0时表示自变量对模型因变量没有影响，其模型的图像为一条直线当x=0时，π(x)\pi(x)= α\alpha表示在没有自变量影响的正常情况下事件发生的概率当π(x)=0.5\pi(x)=0.5时， |β|\left| \beta \right| 最大， x=−α/βx=-\alpha/\beta,这个x值有时被称为中间效应水平，它表示在此水平下每种结果的概率都为50%模型上某一点的切线为βπ(x)[1−π(x)]\beta \pi(x)[1-\pi(x)] ，当概率趋向于0或1时斜率趋向于0，如曲线上 π(x)\pi(x)=0.5,对应的x点处的斜率为β(0.5)(0.5)=0.25β\beta (0.5)(0.5)=0.25\beta ，当其 π(x)\pi(x) =0.9时斜率为0.09 β\beta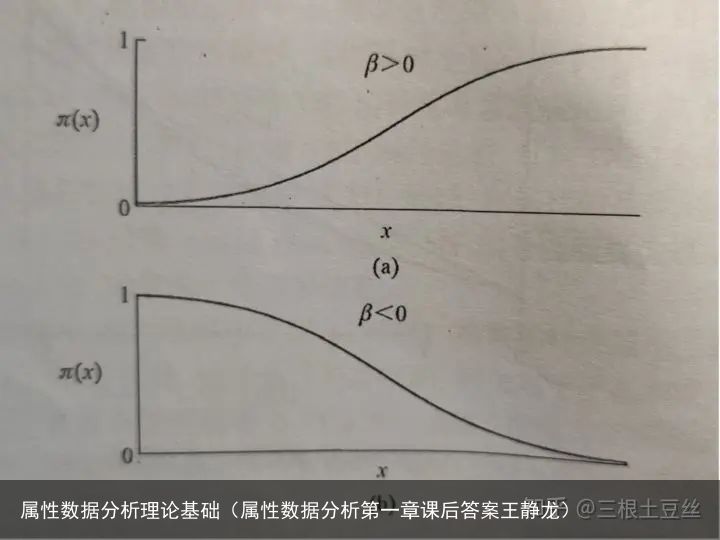

优势：

当其x每增加一个单位，优势变为eβe^\beta 倍，即x+1水平的优势等于 x 水平的优势乘eβe^\beta

例如：

如模型的方程为

模型的方程我们可以通过公式的计算可以得出，从模型方程中我们可以得出

概率估计值函数为 π(x)=−12.3508+0.4972x1+exp(−12.3508+0.4972x)\pi (x) = \frac{-12.3508+0.4972x}{1+exp(-12.3508+0.4972x)} 其中心效应水平为x=−α/β-\alpha/\beta =24.8在点 x = 26.3,的概率估计 π(x)\pi(x) =0.674x每增加一个单位长度，那么应变量事件发生的概率就增加exp( β\beta)=exp(0.4972)=1.64倍

2、多元logistic回归

公式：

参数 βi\beta_i 是控制其它x时 xix_i 对Y=1的对数优势效应，例如固定其他 x 水平时，exp(βi\beta_i)就是xix_i每增加一个单位对于优势的乘积效应

多元logistic回归的大部分特性类似与一元，但是多元logistic回归模型在不同的情况下的定义的不一样的，这里先介绍其较为简单的形式，后期再补充不同类型的logistic模型

模型特点：

控制一个其他自变量不变时相当与一元logistic回归当各自变量不停的改变，得到每种情况下事件发生的概率 π(x)\pi(x)会不一样，在比较时通常采用优势比的形式更能直观的表达

例如：

在一个研究黑人与白人杀人被判死刑的案例中，令 X 被告者种族( x =1 代表白人, x = 0 代表黑人)，Z 受害者种族（z =1 代表白 人, z = 0 代表黑人），得到其logistic拟合模型为

因此，被告为白人且受害者也为白人（ x=1 , z=1）时，被判死刑的概率为 π1=0.1237\pi_1 =0.1237被告为白人且受害者也为黑人（ x=1 , z=0）时，被判死刑的概率为π2=0.0362\pi_2 =0.0362被告为黑人且受害者也为白人（ x=0 , z=1）时，被判死刑的概率为π3=0.1780\pi_3 =0.1780被告为黑人且受害者也为黑人（ x=0 , z=0）时，被判死刑的概率为π4=0.0551\pi_4 =0.0551

从上面的结论中我们可以从其概率上看最有可能让因变量响应为是的条件为π3\pi_3

当控制被告者种族时，受害者种族为白人被判死刑的优势是受害者种族为黑人被判死刑的优势的e1.324e^{1.324} =3.76倍其受害者种族系数的区间估计值为[0.3482,2.4157]，就可以得到其受害者种族间优势比的置信区间[e0.3482,e2.4157]=[1.41,11.20][e^{0.3482},e^{2.4157}]= [1.41,11.20]

3、模型选择策略

1）AIC准则

AIC准则通过比较模型的拟合值和真值(按照某种期望值)的接近程度来评判一个模型。但是，我们更倾向于简约模型，AIC会选取

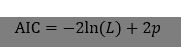
最小化的模型，其中 p 是模型参数个数，L 是最大似然函数。

AIC 越小越好，AIC倾向于选择预测性能最优的模型

2）BIC准则

BIC准则（BIC criterion）又称贝叶斯信息准则，与AIC准则（赤池信息准则）类似，用于模型的选择。BIC会选取

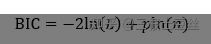
最小化的模型，其中 p 为模型参数个数， n 为样本数量， L为最大似然函数。

BIC 越小越好，BIC倾向于识别真实的模型，选择一个对现有数据拟合最好的模型

示例：

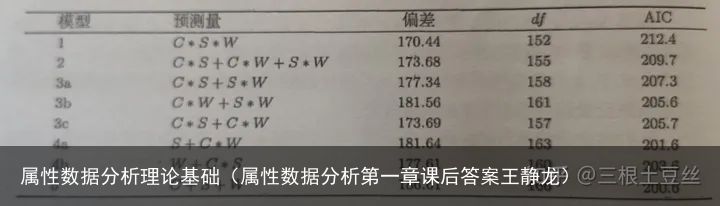
这个模型包含所以三因子交互模型、两因子交互效应和主效应，通过使用逐步变量选择算法一步步选择变量，我们通过举例来看如果确定模型是否能经过一步步的选择检验得到最好的模型

例如我们通过检验其是否存在三项交互项C*S*W，使用假设检验的方法

后续的验证基本一致，就不一一列举

四、多类别logistic模型

logistic回归是对二分响应变量进行建模分析，我们需要对其进行必要的推广让其使用与属性数据和定量数据，使得其有更多可能性

1、名义响应变量logit模型

普通是logistic模型是二项分布的数据，对于多项分布的数据我们使用起来将会有些许困难所以我们推广出了名义响应变量的logit模型，令 J 表示 Y 的类别个数，π1,...,πJ{\pi_1,...,\pi_J}表示响应概率，则 J 种类型的结果的个数的概率分布就是多项分布

适用类型：多分类数据

1）基线-类别logit

在使用名义响应变量的logit模型时我们需要先定义一个基线，其模型是把每个类别与一个基线类别配成对，一般都选择最后一类（ J ）为基线，基线-类别logit为

假设只有一个预测变量x时，基线-类别logit模型为

2）估计响应变量的概率

从上面我们对基线-类别logit的定义中我们也可以发现，其最根本的问题没有得到很好的解决我们所需要的概率 πj\pi_j没有得到很好的体现，所以我们依旧要对其进行转换

分母对每个概率是相同的，分子对各个 j 求和就得到分母

例如：当J=3时，模型利用 log(π1/π3)log(\pi_1/\pi_3) 和 log(π2/π3)log(\pi_2/\pi_3)

我们通过上述的小案例来观其其分析结果，可以得到三类别的属性变量得到的两个方程如下

从而我们也可以得到π1/π2\pi_1/\pi_2 的关系

而我们通过公式得到其三个响应变量的三种类型的概率公式为

2、有序响应变量

有序响应变量势必要比名义响应变量包含更多的信息，所建的模型也将具有更高的功效

适用范围：有顺序区别的多分类数据

1）累计概率

Y 的累积概率是指 Y落在或低于一个特定点的概率。对于结果类别 j，累积概率为

显然地，累积概率满足 P(Y≤1)≤P(Y≤1)≤…≤P(Y≤J)=1，累积概率的模型并不利用最后一个概率，因为它必然等于1，而其最后一个功能相当于基线

2）累计logit

公式：

例如：J=3时有

区别与名义响应变量的模型，在有序模型中每个累积 logit 均利用了所有响应类别

为了更好的说明其模型，我们假设当只有一个预测变量（即自变量）x 的时候，其累计logit模型为

模型中参数 β 描述了 x 对响应变量落在类 j或者小于 j的类的对数优势的效应

注意：模型表达式中参数 β 没有下标，表示模型假设 x 的效应对所有 J-1 个累积 logit 都是相等的，如果模型拟合的好，它只需要一个参数就可以描述 x 的效应，而不需要 J-1 个

累积概率的模型表达式为

3）模型解释

举一个例子来弄懂模型解释：对于 x 的两个值 x_1 和 x_2 ，比较两个累积概率的优势比为

该优势比的对数就是两个 x 值处的累积 logit 的差\beta(x_2-x_1) 有以下结论

与两个 x 值之间的距离成比例p特别地，如果 x_2-x_1=1，那么 x 每增加一个单位，响应变量在任意给定的类别下的优势就应该乘以e^\beta

注意：

比例优势假设：在对数优势比\beta(x_2-x_1)中，相同的比例常数(β)适用于每一个累积概率，这个特性称为模型的比例优势假设。颠倒类别顺序时，会得到相同的拟合，只是 β 的符号相反。拟合过程同时对所有 j 使用了迭代算法。模型中的解释变量可以是定量的，也可以是定性的，或者两者都有

举例：

如上图的模型输出结果， \alpha_1=-2.469则其为当 x=1 的第一个累计概率的估计为

同时我们也可以使用同样的方法计算得到 P(Y\leq2)=0.38 , P(Y\leq3)=0.77 , P(Y\leq4)=0.89，我们算出其累计概率之后，其累计概率的表达式不能直接的表达其含义需要将其修改为P(Y=j) 的形式，即 \pi_1,\pi_2...

的形式，如：

4）模型优化问题

在我们拟合累计概率模型的时候模型很有会出现拟合优度不好、拟合不充分的情况，特别是当响应变量分布具有变异性的时候，那么当我们面对这种问题的时候有三种策略

①利用不同累积概率有不同效应（使用β_j而不是β）的更一般的模型

缺点1：累积概率曲线会在某些预测变量值出现相交。

缺点2：参数数量增加了

②拟合基线-类别logit模型，并以一种非正式的方式在解析关联时利用这个有序性。

缺点1：参数数量增加了

缺点2：模型缺乏精简性，某些感兴趣的量的估计可能会变差

③退化原则: 当响应变量有大量类别时，可以将响应变量的类别归为几个类别

退化成二分变量（普通的logistic回归）

建议：退化成4个类别（效率损失是较小的）

3、成对类别有序

有序响应的累计logit模型在构造每个logit时利用了整个响应量表，有序类别的另一种logit则是利用类别对，一种方法是关于所以的相邻类别对构造logit，即相邻类别logit;另外一种方法是以一种相继的方式来构造有序响应类别的logit，即相继比logit

1）相邻类别logit

相邻类别logit模型更简单的比例优势形式为：

对于该形式，x 对作出更高而不是更低的响应的优势的效应{ { \beta_j=\beta }}，并且每一对相邻响应类别都是相等的,与基线-类别logit模型一样，相邻类别logit决定所有响应类别对的logit

示例：

Y = 政治意识形态（5个类别）

X = 政治党派（民主党 x=0，共和党 x=1）

共和党人的意识形态被分为类 j+1 而不是类 j 的估计优势为民主党人的估计优势的 exp⁡(0.435)=1.54 倍任意两列 a 和 b 的优势比估计等于exp(\beta(a-b))

例如，共和党人的意识形态为类5而不是类1的估计优势为民主党人的估计优势的

exp(\beta(a-b))=exp(0.435\times(5-1))=5.7 倍

2）相继比logit

相继比logit，他们是比较每个类别与来自响应量表的更低水平的组合类别的二分响应

第二种相继比logit模型：

两种相继比logit模型将得到不同的参数估计和拟合优度统计量

4、总结

声明：

本文写作过程中摘录了部分《属性数据分析引论（第二版）》Alan Agresti著，如有侵权或将其删除